Контрольная работа: Проектирование автотранспортных предприятий

Ф(∞) = 1

Формула (2.4) хотя и даёт по сравнению с формулой (2.1) более точные результаты, но также является приближённой. Теорема Бернулли, на которой базируется формула (2.4), справедлива только при значительном количестве опытов (или автомобилей в рассматриваемом случае). Однако уже при наличии 100 однотипных автомобилей в парке формула (2.4) даёт вполне удовлетворительные результаты расчёта.

По формуле (2.4) можно определить потребность в капитальных ремонтах автомобилей не только в течение года, но и за более короткий период эксплуатации, например в течение месяца или квартала. При увеличении планируемого периода эксплуатации необходимо только следить за тем, чтобы пробег автомобилей за этот период был в 2…3 раза меньше межремонтного периода. Другими словами, необходимо, чтобы вероятность выхода автомобиля в ремонт за плановый период более одного раза была ничтожно мала. В противном случае вместо формулы (2.4) применяются известные формулы, также основанные на вероятностных методах расчёта.

Решение.

N_к =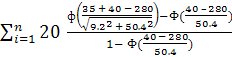 = 20 = 20 = 0,00041

N_к = = 60 = 60 = 0,0246

N_к =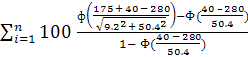 = 100 = 100 = 10,204

N_к =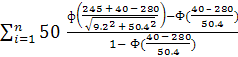 = 50 = 50 = 26,7924

N_к =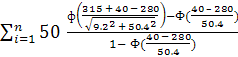 = 50 = 50 = 42,7249

∑N_i = 0 + 0 + 10 + 26 + 42 = 78 тыс. км из 280 тыс. км.

Вывод

Согласно двум методам расчёта получаются близкие величины, вероятностный метод учитывает рассеивание величин пробега l₀ , l_к и l_г , соответственно получается более точным расчёт.

Список используемой литературы

1. Напольский Г.М. Техническое проектирование автотранспортных предприятий СТО/ Г.М. Напольский. – М: Транспорт, 1985.-232с.

2. Краткий автомобильный справочник – М.:Транспорт, 1983.-220с.

3. Техническое обслуживание, ремонт и хранение автотранспортных средств: Учеб. В 3 кн. Организация, планирование и управление /В.Е.Канарчук, А.А.Лудченко, И.П.Курников, И.А.Луйк. – К.: Выща шк., 1991. – Кн.2. – 406 с.