Учебное пособие: Кінематика і динаміка матеріальної точки

Механіка являється однією з наукових основ багатьох областей сучасної техніки. Класичною механікою називають механіку, в основі якої лежать закони Ньютона і предметом якої являється рух макроскопічних тіл зі швидкостями малими в порівнянні зі швидкістю світла.

Рух тіла зі швидкостями, близькими до швидкості світла, вивчається в теорії відносності, а рух мікрочастинок розглядається в квантовій механіці.

Кінематика вивчає рух тіл, не розглядаючи ті причини, які цей рух обумовили.

Динаміка вивчає закони руху тіл і ті причини, що спричиняють чи змінюють цей рух.

Статика вивчає закони рівноваги системи тіл. Статику розглядають як один із випадків динаміки.

Переходимо до розгляду кінематики та динаміки матеріальної точки.

Нехай матеріальна точка переміщується з точки А в точку В (рис.1). Відстань від точки А до точки В, взята вздовж траєкторії, являє собою пройдений шлях S . Вектором переміщення називають відрізок прямої, проведеної з початкового положення в кінцеве положення тіла (вектор ). Якщо тіло перемістилося з точки С в точку В, то другим переміщенням буде вектор . Результуючим переміщенням буде вектор , який дорівнює сумі векторів та , оскільки, як видно з рис.1, відрізок АВ є діагоналлю паралелограма, побудованого на відрізках АС та СВ.

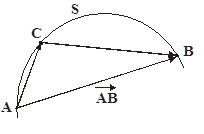
Рис.1

Вектор переміщення співпадає з ділянкою траєкторії лише прямолінійному русі. При криволінійній траєкторії шлях не співпадає з переміщенням. Але, якщо взяти достатньо мале переміщення, то з визначеною точністю можна замінити відрізок шляху DS вектором переміщення . Таке мале переміщення називається елементарним переміщенням.

Шлях, пройдений тілом, являється функцією часу. При рівномірному русі швидкість тіла визначається просто як шлях, пройдений тілом за одиницю часу.

Для більш повної характеристики змінного руху вводять поняття миттєвої швидкості. Якщо за невеликий проміжок часу тіло проходить шлях , то швидкість дорівнюватиме:

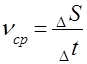(I)

Величина миттєвої швидкості (швидкість в даній точці шляху) рівна границі до якої наближається відношення приросту шляху до відповідного приросту часу при умові, що наближається до нуля.

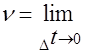
(2)

В математиці ця границя називається похідною від шляху по часу і позначається так:

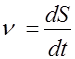(3)

Формулу (3) можна записати і через нескінченно мале переміщення :

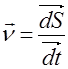(4)

Вектор швидкості співпадає по напрямку з нескінченно малим переміщенням (тобто з дотичною до траєкторії) і чисельно рівний похідній від шляху до часу. В більшості випадків при русі швидкість змінюється і по величині і по напрямку. Для характеристики зміни швидкості вводиться поняття прискорення.

В випадку прямолінійного нерівномірного руху середнє прискорення за проміжок часу D t дорівнює відношенню зміни швидкості до цього проміжку часу.

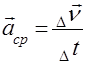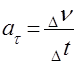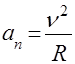; ; (5)

Прискорення, яке тіло має в даний момент (в даній точці шляху) дорівнює границі, до якої наближається права частина рівняння (5) при зменшенні проміжку часу D t до нуля, тобто дорівнює похідній швидкості від часу.

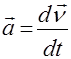(6)

Враховуючи, що швидкість дорівнює похідній шляху по часу, знаходимо, що прискорення дорівнює другій похідній шляху по часу:

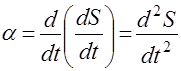(7)

Таким чином, якщо відомий шлях тіла як функція часу, то легко визначити його швидкість і прискорення в будь - який проміжок часу.

З курсу середньої школи відомі ще такі співвідношення кінематики (знайти їх інтегруванням):

; ; 8)