Дипломная работа: Релаксационная стойкость напряжений в металлах и сплавах

Целесообразно различать макрорелаксацию напряжений (в материале, деталях), реализуемую путем макро-ползучести в условиях, затрудняющих изменение линейных размеров детали, и микрорелаксацию напряжений, вызванную процессами микроползучести как между элементами микроструктуры (релаксация 2-го рода), так и внутри их (релаксация 3-го рода). Макрорелаксация напряжений в детали может быть обусловлена процессами микрорелаксации в элементах структуры.

Сопротивление материала релаксации напряжений можно повысить посредством: термической обработки, обеспечивающей оптимальную для релаксационной стойкости структуру; стабилизации, увеличивающей сопротивление релаксации (и ползучести) на первой стадии процесса; термомеханической обработки; повторными нагружениями.

Можно полагать, что получение необходимой информации о характеристиках релаксационной стойкости различных конструкционных материалов в ближайшие годы будет идти двумя путями.

Во-первых, непосредственным испытанием таких материалов на релаксацию напряжений по существующим методикам (включая наиболее распространенный в на­ших лабораториях метод испытания колец равного сопротивления изгибу) при длительностях, отвечающих за­данным срокам службы или приближающихся к ним.

Во-вторых, применением расчетных методов оценки сопротивления релаксации (характеризуемой ползучестью при переменном напряжении) по данным испытаний на ползучесть (при постоянном напряжении). Например, характеристики релаксации для условий однократного нагружения можно с достаточной точностью рассчитывать по теориям упрочнения или течения. Распространение электронных вычислительных машин позволит широко использовать для определения характеристик релаксации первичные кривые ползучести материалов. Оба эти направления являются правомерными и отнюдь не исключают друг друга.

Так, если сплав разрабатывается или исследуется для деталей, работающих в условиях жесткого нагружения (возможной релаксации напряжений), то целесообразно проводить испытание не на ползучесть, а на релаксацию, поскольку последнее значительно менее трудоемко, особенно если испытывать кольца равного сопротивления изгибу (по И.А. Одингу) или винтовые пружины (по А.А. Чижику). В последнем случае результаты испыта­ний па релаксацию используют даже для расчетного определения характеристик ползучести. Кроме того, поскольку предложенные расчетные методы определения сопротивления повторной релаксации не нашли еще достаточно широкого применения, проведение соответствующих испытаний для оценки этой характеристики является совершенно необходимым.

1 Физическая природа и механизмы релаксации напряжений в металлах и сплавах

Кристаллическое тело, переведенное воздействием внешних сил в неравновесное состояние, всегда стремится возвратиться обратно в равновесное состояние. Процесс перехода кристаллического тела из неравновесного состояния в равновесное называют релаксационным.

В идеальном (бездефектном) монокристаллическом теле все процессы, вызванные воздействием внешних сил, обратимы. Но без освобождения тела от действия внешних сил стремление к возвращению в равновесное состояние в идеальных кристаллах может реализоваться только в условиях, при которых атомы под влиянием флуктуации тепловой энергии преодолевают энергетический барьер, или в том случае, если монокристалл дробится на субзерна. В реальных кристаллах релаксационные процессы обусловливаются наличием дефектов кристаллической решетки.

При упругом деформировании кристаллических тел с любой конечной скоростью уровень свободной энергии повышается и они переходят в термодинамически неравновесное состояние. Только в идеально упругом теле при бесконечно медленном (квазистатическом) деформировании в условиях низких напряжений не будет происходить рассеяние упругой энергии и упругое деформирование будет полностью обратимым процессом, для которого справедлив приближенный закон Гука: .

Для реальных кристаллических тел, нагруженных в упругой области, эта зависимость, строго говоря, неприемлема, так как благодаря наличию дефектов в них почти всегда наблюдается переход из термодинамически неравновесного в более равновесное состояние. Такие отклонения от упругого поведения обычно называют общим термином «упругие несовершенства» или «явления неупругости». Процессы неупругости, развивающиеся во времени в направлении к равновесному состоянию, являются релаксационными.

Релаксационные процессы развиваются по-разному в зависимости от свойств тела, вида деформации и условий, в которых они протекают, и проявляются в виде упругого последействия, внутреннего трения, релаксации напряжений.

1.1 Явление релаксации напряжений

Еще в первой половине прошлого столетия были отмечены факты самопроизвольного уменьшения внутренних напряжений. По мнению Пуассона, в жидкостях в течение некоторого времени непрерывно выравниваются или ослабляются напряжения от внешнего давления. Распространив эту мысль на твердые тела, К.Максвелл сделал предположение, что спадание (или релаксация) напряжений в функции времени пропорционально величине напряжения. Он рассматривал твердое тело как упруго-вязкую систему, сочетающую в себе идеально упругое тело Гука и идеально вязкое тело Ньютона. Следовательно, по Максвеллу изменение (релаксация) напряжения во времени должно следовать закону:

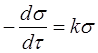(1)

где константа, характеризующая скорость релаксации;

Е— модуль упругости;

—коэффициент вязкости.

После интегрирования в пределах от 0 до τ при начальных условиях τ=0; получаем

(2)

Величину, обратную k, Максвелл назвал «временем релаксации» . Тогда уравнение (2) можно представить в виде

(3)

Здесь — время, в течение которого начальное напряже­ние убывает в e=2,71828 раз.

Помимо модели Максвелла (рисунок 1,а), состоящей из последовательно соединенных элементов: упругого Е и вязкого η, для описания процессов ползучести используют модель Кельвина-Фойгта (рисунок 1,б), состоящую из параллельно соединенных элементов Е и η, а также комбинации моделей Кельвина-Фойгта, Максвелла и упругих элементов. Так, при описании ползучести и релаксации, согласно комбинированной гипотезе ползучести, предложенной Е. А. Хейном, использована модель рисунок 1,в. Она состоит из звена Максвелла, описывающего необратимую ползучесть, и совокупности звеньев Кельвина-­Фойгта, моделирующих упругое последействие.

Н. С. Курнаков рассматривал явление релаксации напряжений в тесной связи с природой и свойствами испытуемого материала и его состоянием. Наблюдая во время опытов по изучению давления истечения пластических тел за процессом изменения напряжения во времени, он пришел к выводу, что скорость релаксации k (а следовательно, и время релаксации ) зависят не только от внешних условий (температуры, давления и др.), но и от природы металла и его предварительной обработки.

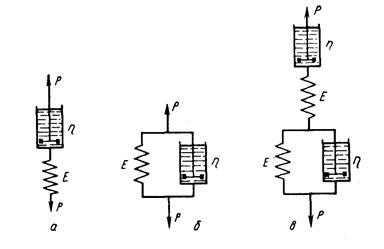
Рисунок 1 – Модели твердого тела

Н.С. Курнаков придавал большое значение явлению релаксации напряжений и даже включил «время релаксации» в число свойств, определяемых при физико-химическом анализе металлов и сплавов.

Основные идеи Н.С. Курнакова впоследствии были развиты при изучении физической природы релаксации напряжений С. И. Губкиным, Л. В. Шведовым и другими исследователями.

В частности, С.И. Губкин [2] высказал мысль, что в поликристаллическом металле скорость релаксации напряжений зависит от скорости межзеренных скольжений и внутрикристаллических сдвигов. Это положение было позднее развито и значительно дополнено И. А. Одингом. Далее, скорость процессов релаксации обусловлена не только скоростью деформации, но прежде всего является функцией состояния самого вещества.

Как уже упоминалось, релаксация напряжений — процесс самопроизвольного снижения напряжения в теле, поставленном в условия неизменности начальной деформации в направлении действия силы. Эти напряжения могут быть специально созданы при сборке узлов машин или приборов, например болтовые соединения, цилиндрические и ленточные пружины, сохраняющие свои размеры в процессе работы, различные тугие посадки и т.д., а также находящий все более широкое применение напряженный бетон, армированный предварительно напряженной проволокой. Во всех этих случаях желательно возможно дольше сохранить близкий к начальному уровень напряжений и поэтому их релаксация нежелательна.