Доклад: Классификация объектов нечисловой природы на основе непараметрических оценок плотности

где -объем шара единичного радиуса в .

Поскольку можно записать, что

где

то переход от к соответствует переходу от к . Выгода от такого перехода заключается в том, что утверждения приобретают более простую формулировку.

ТЕОРЕМА 1. Пусть - естественная метрика,

Плотность непрерывна в и ограничена на , причем . Тогда , оценка является состоятельной, т. е. по вероятности при ,

Теорема 1 доказана в [4]. Однако остается открытым вопрос о скорости сходимости ядерных оценок, т. е. о поведении величины

и об оптимальном выборе показателей размытости .

Введем круговое распределение и круговую плотность .

ТЕОРЕМА 2. Пусть ядерная функция непрерывна и при . Пусть круговая плотность допускает разложение

причем остаточный член равномерно ограничен [0, 1,...., ]. Пусть

Тогда

Величина достигает минимума, равного

при

что совпадает с классическими результатами для (см. [9, с316]). Заметим, что для уменьшения смещения оценки приходится применять знакопеременные ядра .

В случае дискретных пространств естественных метрик не существует. Однако можно получить аналоги теорем 1 и 2 переходя к пределу не только по объему выборки , но и по параметру дискретности .

Пусть - последовательность конечных пространств, - расстояния в

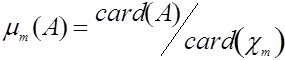для любого .

Положим

,

,

,

Тогда функции кусочно постоянны и имеют скачки в некоторых точках , причем .

ТЕОРЕМА 3. Если при (другими словами, при ), то существует последовательность параметров дискретности такая, что при , , справедливы заключения теорем 1 и 2.

ПРИМЕР 1. Пространство всех подмножеств конечного множества из элементов допускает [10, Пар 4. 3] аксиоматическое введение метрики 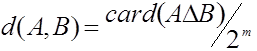, где - символ симметрической разности множеств. Рассмотрим непараметрическую оценку плотности типа Парзена - Розенблатта 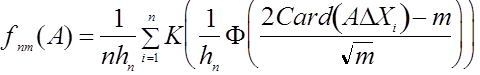, где - функция нормального стандартного распределения. Можно показать, что эта оценка удовлетворяет условиям теоремы 3 .

ПРИМЕР 2. Рассмотрим пространство функций , определенных на конечном множестве 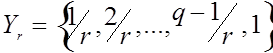со значениями в конечном множестве . Это пространство можно интерпретировать как пространство нечетких множеств [11]. Очевидно, . Будем использовать расстояние . Непараметрическая оценка плотности имеет вид: .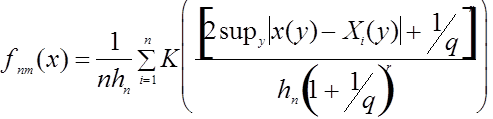

Если , , то при выполнены условия теоремы 3, а потому справедливы теоремы 1 и 2.

. ПРИМЕР 3. Рассматривая пространства ранжировок объект непреов, в качестве расстояния между ранжировками и . Тогда . не стремиться к 0 при ., условия теоремы 3 не выполнены.

Пространства разнотипных признаков - это декартово произведение непрерывных и дискретных пространств. Для него возможны различные постановки. Пусть, например, число градаций качественных признаков остается постоянным. Тогда непараметрическая оценка плотности сводится к произведению частоты попадания в точку в пространстве качественных признаков на классическую оценку Парзена-Розенблатта в пространстве количественных переменных. В общем случае расстояние можно, например, рассматривать как сумму евклидова расстояния между количественными факторами, расстояния между номинальными признаками (, если и , если ) и расстояния между порядковыми переменными (если и - номера градаций., то .

Наличие количественных факторов приводит к непрерывности и строгому возрастанию , а потому для непараметрических оценок плотности в пространствах разнотипных признаков справедливы теоремы 1 - 3.

Литература

1.Орлов А.И. Устойчивость в социально-экономических моделях.-М.Наука,1979.-296 с.