Книга: Функция yax2bxc

Учитель : Приступим к изучению нового материала. Откройте тетради, запишите число и тему урока. Обратите внимание на доску.

Запись на доске : Число.

Функция .

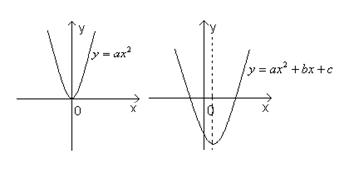
Учитель : На доске вы видите два графика функций. Первый график , а второй . Давайте попробуем сравнить их.

Свойства функции вы знаете. На их основании, и сравнивая наши графики, можно выделить свойства функции .

Итак, как вы думаете, от чего будет зависеть направление ветвей параболы ?

Ученики: Направление ветвей обеих парабол будет зависеть от коэффициента .

Учитель: Совершенно верно. Так же можно заметить, что у обеих парабол есть ось симметрии. У первого графика функции, что является осью симметрии?

Ученики: У параболы вида осью симметрии является ось ординат.

Учитель: Верно. А что является осью симметрии параболы

?

Ученики: Осью симметрии параболы является линия, которая проходит через вершину параболы, параллельно оси ординат.

Учитель : Правильно. Итак, осью симметрии графика функции будем называть прямую, проходящую через вершину параболы, параллельную оси ординат.

А вершина параболы – это точка с координатами . Они определяются по формуле:

Запишите формулу в тетрадь и обведите в рамочку.

Запись на доске и в тетрадях

- координаты вершины параболы.

Учитель : Теперь, чтобы было более понятно, рассмотрим пример.

Пример 1 : Найдите координаты вершины параболы .

Решение: По формуле

имеем:

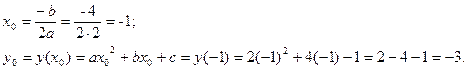
Ответ: координаты вершины параболы.

Учитель : Как мы уже отметили, ось симметрии проходит через вершину параболы. Посмотрите на доску. Начертите этот рисунок в тетради.

Запись на доске и в тетрадях: