Контрольная работа: Графы и частично упорядоченные множества

Любое у-множество можно представить как ориентированный граф, в котором дуга a®b между парой элементов означает a£b. Однако не любой ориентированный граф является представлением у‑множества. Чтобы сугубо ориентированный граф представлял правильное у‑множество, необходимо и достаточно чтобы в нем не было циклов.

В математической литературе у-множества обычно изображаются в виде неориентированных графов (рис.2), при этом подразумевается, что предшествующие элементы расположены ниже последующих. Поэтому, если в этих схемах правильно заменить ребра на дуги, то все дуги окажутся направленными снизу вверх.

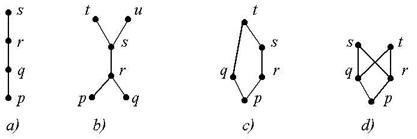
Рис.2

На этих рисунках показаны не все связи между элементами - те, которые следуют из свойства транзитивности (например, связь p®s на каждом из этих рисунков), в них отсутствуют. Такое сокращенное представление у‑множеств без транзитивных связей называется диаграммой Хассе.

В дальнейшем мы будем изображать частично упорядоченные множества не так как это принято в математических работах по алгебре (см. рисунок 2), а в виде ориентированных графов. Определим наименьший и наибольший элементы у-множеств.

Наименьшим элементом у-множества M (если он существует) называется элемент y такой, что y£a для любого элемента aÎM.

Наибольшим элементом у-множества M (если он существует) называется элемент y такой, что a£y для любого элемента aÎM

Например, в у-множестве, изображенном на рис.2, b, нет ни наибольшего, ни наименьшего элементов, наименьший элемент (p) имеется в у‑множествах, изображенных на рис.2, a, c, d, а наибольший элемент имеется только в у‑множествах, изображенных на рисунке 2, a, c.

Если в качестве отношения частичного порядка мы выберем отношение включения, то в этом отношении наименьшим элементом является пустое множество (Æ) (оно включено в любое множество), а наибольшим является универсум (в него включено любое множество системы).

Рассмотрим два очень важных понятия теории у-множеств, которые позволяют существенно облегчить решение некоторых задач анализа рассуждений. Это верхние и нижние конусы. Пусть A - произвольное подмножество у‑множества M (т.е. AÍM). Определим для множества A верхний и нижний конусы.

Нижним конусом множества A называется множество всех таких элементов x, принадлежащих множеству M, каждый из которых будет меньше или равен (£) относительно любого элемента a, принадлежащего множеству A.

Верхним конусом множества A называется множество всех таких элементов x, принадлежащих множеству M, для каждого из которых любой элемент из множества A будет меньше или равен (£) ему.

Нижний и верхний конусы можно определять не только для подмножеств, но и для элементов у‑множества M. Если у-множество изображено в виде ориентированного графа, то верхний и нижний конус для любого элемента X можно "вычислить", используя свойство достижимости:

верхний конус элемента X- это множество элементов, в это множество входит сам элемент X и все элементы, достижимые из X;

нижний конус элемента X- это множество элементов, в это множество входит сам элемент X и все элементы, из которых X достижимо.

Например, на множестве чисел M = {2, 4, 5, 7}, упорядоченном по величине, нижним конусом числа 4 является множество {2, 4}, а верхним - {4, 5, 7}. Если рассмотреть у‑множество, показанное на рисунке 9, b, то

={p, q, r} и = {r, s, t, u}.

Далее мы рассмотрим две теоремы, связанные с конусами. C помощью первой теоремы можно вычислить верхние и нижние конусы не для отдельных элементов, а для некоторых их совокупностей. По смыслу верхние конусы для некоторого множества M элементов должны содержать такие элементы, которые одновременно достижимы из каждого элемента множества M. Аналогично, если вычисляется нижний конус для множества M, то он должен содержать такие элементы, каждый из которых предшествуют любому элементу из множества M. Тогда верхний и нижний конусы для этого множества вычисляются в соответствии со следующей теоремой.

Теорема. Пусть в произвольном у-множестве выбрано некоторое подмножество M = {q₁ , q₂ ,... q_n } его элементов. Тогда

(i) M^D = ÇÇ... Ç;

(ii) M^Ñ =ÇÇ... Ç.

Доказательство. Пусть m_i - произвольный элемента множества M^D . Чтобы для каждого q_k (q_k ÎM) соблюдалось условие q_k £m_i , необходимо и достаточно, чтобы элемент m_i содержался в верхнем конусе каждого из элементов множества M. А это означает, что элемент m_i содержится в пересечении ÇÇ... Ç верхних конусов всех этих элементов. Аналогично, если m_i - произвольный элемента множества M^Ñ , то для каждого q_k (q_k ÎM) соблюдается условие m_i £q_k , а это означает, что элемент m_i содержится в нижнем конусе каждого из элементов множества M. Следовательно, все элементы множества M^Ñ должны находиться в пересечении ÇÇ... Ç нижних конусов. Конец доказательства.

Для лучшего понимания соотношений, связанных с конусами, рассмотрим граф, изображающий диаграмму Хассе некоторого у-множества (рисунок 3).

Рис.3

По этому рисунку можно, используя свойство достижимости, легко вычислить верхние и нижние конусы любых элементов. Например,

R^D = {R, G, F, Q}

(элемент R содержится в верхнем конусе по определению, а остальные элементы введены как достижимые из R);