Контрольная работа: Машины и их основные элементы

Рис. 1.4. Схема зубчатой передачи:
I—шаг зацепления; h — высота зуба; h' — высота головки зуба; h» — высота ножки зуба; ЙЦ2) — диаметр делительной окружности; dn^) —диаметр окружности впадин; d . —диаметр окружности выступов
Передаточное число зубчатой передачи
![]()
где 21( z2 — число зубьев соответственно ведущего и ведомого колес.
Толщина зуба и ширина впадины, измеренные по дуге окружности, не являются постоянными. У основания зуба его толщина максимальна, а ширина впадины — минимальна, у вершины зубьев— наоборот . Окружность, по которой толщина зуба равна ширине впадины, называется начальной. При нарезке зубьев нормального зацепления эту окружность используют для настройки станка. По этой причине ее также называют делительной.
Зубчатые передачи характеризуются шагом t и модулем m = tjn.
Шагом зубчатого зацепления называют расстояние между одноименными профилями (правым и левым) двух соседних зубьев, измеренное по дуге начальной окружности .
Модуль зубчатого зацепления m измеряется в миллиметрах. Значения модулей стандартизованы. Все размеры зубчатого колеса принято выражать в долях модуля.
В зависимости от формы колес зубчатые передачи бывают цилиндрические и конические , в зависимости от расположения зубьев — прямозубые , косозубые и шевронные (угловые) .

Зубчатые передачи наиболее распространены, так как обеспечивают постоянное передаточное число, высокий КПД, возможность передачи больших усилий, имеют малые габариты. К недостаткам передач относятся сложность изготовления и небольшое межосевое расстояние.
Червячную передачу образуют червяк и червячное колесо. Червяк — это винт с трапецеидальной резьбой. Он бывает однозаходный и многозаходный. Червячное колесо — цилиндрическое колесо, снабженное косыми зубьями, имеющими впадину на середине обода. Движение в червячной передаче осуществляется от червяка к колесу.
Передаточное число червячной передачи определяется как отношение числа зубьев колеса zK к числу заходов червяка z4 :
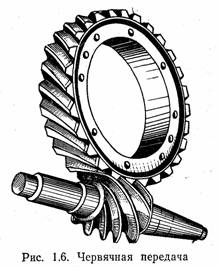
Главные достоинства червячной передачи — возможность полу-ения больших передаточных чисел (до 200), плавность в работе бесшумность. Червячные передачи с небольшим числом заходов червяка обладают свойством самоторможения, т. е. вращение от червячного колеса не может передаваться червяку. Это свойство часто используют в подъемных механизмах небольшой грузоподъемности, например в червячных талях.
Они служат для понижения частоты вращения и увеличения вращающих моментов. В зависимости от числа зубчатых передач редукторы бывают одно-, двух- и трехступенчатые. Передаточное число редуктора равно произведению передаточных чисел каждой пары. В зависимости от формы колес они бывают цилиндрические, конические, коническо-цилиндрические, червячные.
Цепные передачи состоят из ведущей и ведомой звездочек, охватываемых бесконечной цепью. Они применяются для передачи момента вращения между параллельными валами, находящимися на значительном расстоянии. В отличие от ременных цепные передачи могут передавать значительно большую мощность.
Передаточное число цепной передачи определяется как отношение числа зубьев ведомой звездочки к числу зубьев ведущей звездочки. Звездочки цепных передач по конструкции напоминают зубчатые колеса, но имеют другой профиль зубцов. Цепи бывают втулочные, роликовые и зубчатые. Для нормальной работы передачи цепи должны иметь предварительное натяжение. В процессе эксплуатации они требуют периодической смазки.
2. Плоская система сил
Частный случай общей поставки задачи.
Пусть все действующие силы лежат в одной плоскости – например, листа. Выберем за центр приведения точку О – в этой же плоскости. Получим результирующую силу ![]() и результирующую пару
и результирующую пару ![]() в этой же плоскости, то есть
в этой же плоскости, то есть
![]()
3. Кручение
Распределение напряжений при кручении
Деформация кручения возникает, как было отмечено ранее, при действии на брус нагрузок, создающих противоположные пары сил в плоскостях, перпендикулярных продольной оси бруса. Так как при этом прямолинейные образующие круглого бруса принимают вид винтовых линий (это легко наблюдать на резиновом стержне), то можно предположить, что при кручении каждое поперечное сечение по отношению к соседнему поворачивается на некоторый угол. Можно также представить, что брус сложен из множества тончайших дисков; при повороте каждого из них на стыке с соседним происходят перемещения точек в плоскостях, перпендикулярных оси бруса. Вывод таков: при кручении бруса в каждом сечении происходит деформация сдвига и возникают касательные напряжения. Однако, если при сдвиге все точки деформируемого сечения прямолинейно смещались на равные расстояния, то при кручении материал в разных точках, находящихся на разных расстояниях от оси бруса, испытывает разные деформации. Чем дальше точка удалена от оси, тем больше перемещение по дуге. Но так как по закону Гука напряжения прямо пропорциональны относительной деформации, то очевидно, что и напряжения в различных точках одного и того же сечения будут различны и прямо пропорциональны расстоянию точки от центра сечения, называемого полюсом. В точке сечения, совпадающей с полюсом, напряжение будет равно нулю, а наибольшие напряжения тmax возникают в наиболее удаленных от полюса точках, расположенных на поверхности бруса. Таким образом, первое различие деформаций кручения и сдвига заключается в различных законах распределения напряжений по сечению. Второе различие состоит в том, что использование метода сечений при сдвиге позволяет выявить равнодействующую внутренних сил (поперечную силу Q), а при кручении тот же метод приводит к обнаружению равнодействующей пары сил, создающей внутренний крутящий момент Т. Оба различия деформаций необходимо иметь в виду при определении действительных напряжений при кручении. Вывод расчетной формулы для определения действительных напряжений в опасных точках сечения скручиваемого бруса (тmах) достаточно сложен и требует большого числа математических преобразований, но основывается он на известных положениях. Их последовательность, соответствующая порядку действий при математических преобразованиях, такова. В любом сечении скручиваемого бруса должен действовать внутренний крутящий момент сил упругости, равный внешнему вращающему моменту и возникающий следующим образом: в каждой точке деформируемого сечения действует касательное напряжение, по закону Гука прямо пропорциональное относительной деформации; если предположить, что в окрестностях точки, т. е. на очень маленькой площадке, это напряжение остается неизменным, то это равносильно тому, что в сечении действуют элементарные касательные внутренние силы, каждая из которых создает относительно оси бруса (полюса сечения) элементарный внутренний момент: сумма этих элементарных моментов и является внутренним крутящим моментом. Соответствующие приведенным рассуждениям математические преобразования (при условии, что брус имел круглое поперечное сечение диаметром d) приводят к формуле тmax = T/(п * d^3 / 16) Выражение (пd^3)/16 называют полярным моментом сопротивления сечения кручению и обозначают Wp (размерность — м3, см3 или мм3). Для практических расчетов можно принять, что пd^3/16~=0,2d^3 . Сравнение формул для определения действительных напряжений при сдвиге (тср = Q/S) и кручении (тmах = = T/Wp) позволяет сделать вывод, что в правых частях приведенных равенств числитель отражает внутренний силовой фактор, а знаменатель — геометрический. Таким образом, числовая величина Wp характеризует способность бруса, имеющего круглое поперечное сечение заданных размеров, сопротивляться деформации кручения.
Расчеты на прочность
Типовой деталью, испытывающей деформацию кручения, является вал. При проектном расчете его на прочность надо по предварительно выявленному крутящему моменту и допускаемому напряжению определить необходимый диаметр вала. Исходной является зависимость, в которой, как обычно, в качестве максимальных действительных напряжений используются допускаемые напряжения. Так как для валов многих машин бывает известен не внешний момент, а передаваемая мощность Р (Вт) и угловая скорость w (1/с) или частота вращения n (об/мин или об/с) вала, то прежде всего определяют внешний вращающий момент. Если числовая величина n дана в об/мин, то w = пn/30, если в об/с, то w = 2пn. При проверочном расчете, как и в случаях других деформаций, определяют действительные напряжения и сравнивают их с допускаемыми. Прочность будет обеспечена, если соблюдается условие тк = T/(0,2d^3)<=[тк].
Список использованной литературы
1. www . motozavr . ru .