Контрольная работа: Моделирование электрических цепей при помощи программы Micro-Cap
RLC-цепь характеризуется следующими параметрами:
![]() - резонансная частота цепи (рад/с);
- резонансная частота цепи (рад/с);
![]() - декремент затухания, определяет скорость спада свободных колебаний в цепи;
- декремент затухания, определяет скорость спада свободных колебаний в цепи;
![]() - частота свободных колебаний цепи (рад/с);
- частота свободных колебаний цепи (рад/с);
![]() - добротность RLC-цепи.
- добротность RLC-цепи.
Частота f, выраженная в герцах, связана с круговой частотой ω известным соотношением: f = ω/2π [Гц].
При Q < 0,5 переходные процессы в цепи носят апериодический характер. Например, в схеме, приведенной на рис. 9, а, заряженный предварительно от источника V1 конденсатор C1 будет разряжаться через последовательно соединенные индуктивность L1, резистор R1 и внутреннее сопротивление источника (равное нулю). Энергия, накопленная в конденсаторе, будет полностью рассеяна в резисторе R1.
При Q > 0,5 RLC-цепь имеет режим свободных колебаний. Т.е. после окончания воздействия импульсного сигнала в RLC-цепи начинается колебательный процесс. В схеме рис. 9, а энергия, накопленная в конденсаторе (энергия электрического поля) в процессе его разряда перейдет в энергию магнитного поля индуктивности, что в свою очередь, вследствие самоиндукции, приведет к перезарядке конденсатора и т.д. Возникшие в RLC-цепи колебания напоминают колебания механического маятника, которые постепенно затухают из-за потерь при трении в подвеске маятника. Подобную роль в RLC цепи выполняет сопротивление резистора R1, препятствующего протеканию тока в контуре. При ![]() запас энергии, накопленный в цепи, в процессе возникших колебаний будет рассеиваться в сопротивлении R1, постепенно снижаясь до нуля.
запас энергии, накопленный в цепи, в процессе возникших колебаний будет рассеиваться в сопротивлении R1, постепенно снижаясь до нуля.
В случае, когда добротность контура Q >> 1, возникшие в RLC цепи колебания носят устойчивый и продолжительный характер. В колебательном контуре отдельный резистор, как правило, отсутствует, однако при анализе схемы сопротивление R, обусловленное потерями в индуктивности, конденсаторе и монтажных проводниках, необходимо учитывать. Чем меньше сопротивление потерь, тем более узкополосным является фильтр.

Рис. 5
На рис. 5, а показаны диаграммы изменения падения напряжения на конденсаторе С1 и тока, протекающего в последовательном контуре (рис. 4, а) в режиме свободных колебаний при Q >> 1. Из рис. 5, а следует, что полученные гармоники сдвинуты относительно друг друга по фазе на 900 : при максимальном (по модулю) падении напряжения на конденсаторе ток в цепи равен нулю, а при максимальном токе -напряжение на конденсаторе равно нулю (т.е. конденсатор полностью разряжен).
На рис. 5, б изображены АЧХ и ФЧХ последовательного контура (выходное напряжение снимается с узла 2 схемы рис. 4, а). На резонансной частоте (f0 = 3,183 МГц) коэффициент передачи цепи близок к нулю, поэтому такой фильтр называют режекторным. Полоса режекции фильтра по уровню 0,707 составляет 31,83 кГц. Для измерения полосы режекции (или полосы пропускания фильтра, показанного на рис. 4, б) и нанесения на график горизонтальной размерной линии необходимо в режиме электронного курсора воспользоваться командами GotoY (![]() ) и Tag Horizontal.
) и Tag Horizontal.
3. Элементы нелинейных цепей
В линейных цепях параметры используемых элементов (резисторы, конденсаторы, индуктивности) не зависят от значений приложенных к ним напряжений или протекающего через них тока. Однако линейная теория анализа цепей оказывается справедливой только в определенных пределах этих значений. Так, сопротивление R= 10 Ом означает, что отношение падения напряжения на элементе к протекающему через него току равно десяти, независимо от величины этого тока. В действительности же любой реальный элемент таким постоянством не обладает. Например, сопротивление реальных резисторов зависит от температуры, которая в свою очередь определяется не только окружающей средой, но и тепловой энергией, рассеянной в резисторе за счет протекающего через него тока.
На практике при анализе линейных цепей непостоянством параметров элементов цепи часто пренебрегают в силу незначительности их изменений. В частности, зависимость сопротивления резистора от тока можно существенно уменьшить, если при проектировании схемы применить в электрической схеме резистор, способный рассеять расчетную мощность, преобразованную в теплоту. Тогда температура резистора, а значит и его сопротивление, будет определяться в основном температурой окружающей среды, т.е. условиями эксплуатации проектируемого устройства.
Существует обширный класс радиотехнических элементов и устройств, параметры которых существенно зависят от токов или напряжений. Такие элементы называются нелинейными (НЭ) и широко используются в радиотехнике. Для количественного описания свойств НЭ необходимо задать зависимости, определяющие связь между параметром элемента и величиной приложенного напряжения или тока. Такие зависимости принято называть характеристиками нелинейного элемента. В зависимости от типа характеристики можно выделить следующие простейшие нелинейные элементы.
Нелинейный резистивный элемент – полностью определяется зависимостью между током и напряжением: i=f(u) или u=f(i). Данная зависимость называется вольт-амперной характеристикой (ВАХ) нелинейного элемента. Примерами резистивных НЭ являются диоды, стабилитроны, варисторы и др.
Нелинейная емкость – характеризуется нелинейной зависимостью накопленного заряда от приложенного напряжения, т.е. по сути, зависимостью емкости элемента от напряжения: C=f(u), называемой вольт-фарадной характеристикой. В качестве примера элемента с нелинейной емкостью следует назвать варикап, который широко используется в радиоприемных и передающих устройствах для изменения резонансной частоты колебательных контуров.
Нелинейная индуктивность – характеризуется нелинейной связью потокосцепления и тока, которая задается функцией: L=f(i).
В качестве примера более сложного нелинейного устройства следует отметить транзисторы, которые относятся к классу безынерционных нелинейных четырехполюсников (рис.6). В этих полупроводниковых приборах выходной ток (в случае биполярного транзистора - ток коллектора) является сложной функцией не только напряжения, приложенного к коллектору, но и тока в базе транзистора.
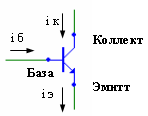
Рис. 6
Нелинейность характеристик рассмотренных выше элементов принципиальна для их функционирования в составе соответствующих электронных устройств
4. Основные этапы моделирования
1. Моделирование схем с резистивным НЭ
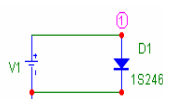
Рис. 7
1.1. Собрать схему, показанную на рис.7. Выбрать одну из доступных моделей диодов, например 1S2460. В режиме DCAnalysis задать параметры для первой варьируемой переменной: Method – Auto, Name – V1, Range – 2 (изменение переменной V1 в диапазоне 0…2 В). В качестве независимой переменной указать напряжение на аноде диода V(1), а в окне XExpression задать переменную I(D1). Включите опцию AutoScaleRanges и построить ВАХ. Используя режим электронного курсора (CursorMode), измерить сопротивление диода на линейном участке ВАХ. Для этого расположить левый и правый курсоры на линейном участке полученного графика на некотором расстоянии друг от друга. Параметр Slope (тангенс угла) для переменной I(D1), который в режиме CursorMode находится в нижней части окна графиков, по сути, определяет проводимость диода, а сопротивление – это величина, обратная проводимости.