Контрольная работа: Моделирование систем
Задание 4
С помощью карт Карно найти минимальную КНФ и ДНФ функции:
![]()
Решение
Запишем карту Карно:
| zt | 00 | 01 | 11 | 10 |
| xy | ||||
| 00 | 1 | 1 | 0 | 0 |
| 01 | 1 | 0 | 0 | 0 |
| 11 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 1 | 0 |
Минимальные формы:
КНФ (покрытия по нулям): ![]()
ДНФ (покрытия по единицам): ![]()
Задание 5
Придумать связный ориентированный граф из пяти вершин и не менее чем семи ребер (ориентированы могут быть не все ребра). Для данного графа составить структурную матрицу, по ней (методами булевой алгебры) найти все пути и сечения между двумя любыми несмежными вершинами на ваш выбор
Решение
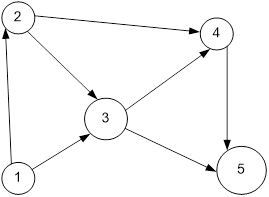
Таблица:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 |
Пути из 1 в 4:
1. 1-3-4
2. 1-2-4
Задание 6
Придумать связный взвешенный граф из восьми вершин и не менее чем 14 ребер (нумерация ребер – слева направо, веса от 1 до 20). Для этого графа построить минимально островное дерево с помощью алгоритма Прима, и найти расстояние между вершинами 1 и 8 с помощью алгоритма Дейкстры. Реализовать алгоритм на любом языке программирования.
алгебра логика графполином дейкстра
Решение
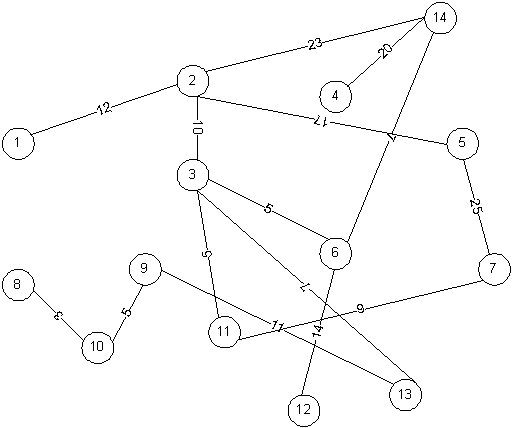
Текст программы для алгоритма Дейкстра
//---------------------------------------------------------------------------
#include <clx.h>
#pragma hdrstop
//---------------------------------------------------------------------------
#pragma argsused
//Нахождение расстояния от источника до всех вершин в графе
//с неотрицательными весами (метод Дейкстры).