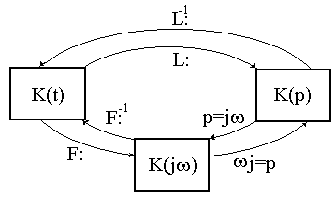
Рис. 3

Преобразование Фурье. Соответствие между временным и частотным представлением сигнала можно выразить через преобразование Фурье:

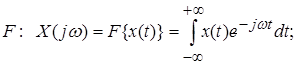(2.1)

и обратное преобразование Фурье:

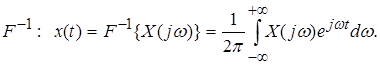(2.2)

Преобразование Лапласа. Соответствие между временным и операторным представлением сигнала можно выразить через преобразование Лапласа:

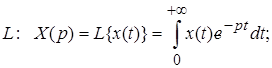(2.3)

и обратное преобразование Лапласа:

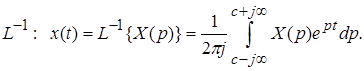(2.4)

где р = c+ j w – оператор Лапласа, c – область сходимости, x(t) – оригинал, а X(p) – изображение.

Для дискретных систем используют дискретные преобразования Лапласа и Фурье, а также ряд других преобразований (Z, W и др.).

Основные свойства (теоремы) преобразования Лапласа

Свойство линейности

(2.5)

2. Дифференцирование оригинала

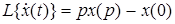, (2.6)

,

где.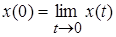

При нулевых начальных условиях

.

3. Интегрирование оригинала

. (2.7)

4. Теорема о свертке (умножения в комплексной области)

. (2.8)

5. Теорема разложения.

Если где

то оригинал, в соответствии с теоремой Коши о вычетах может быть определен как сумма вычетов по полюсам подынтегральной функции

(2.9)

6. Теорема о предельных значениях функции.

Начальное значение функции:. (2.10)

Конечное значение функции: . (2.11)

7. Теорема запаздывания

. (2.12)

4. Дифференциальные уравнения САУ