Контрольная работа: Травление и формовка анодной алюминиевой фольги

l – номер ряда агрегатов;

k – условие неоднородности оцениваемое по фактору В_ф (k = 1–3)

Для этих математических моделей однородных компонент коэффициенты множественной корреляции соответственно равны R _{Н 1} = 0,887, R _Н2 = 0,92, R _Н3 = 0,87, что значительно выше критических значений (говорит о том, что все неоднородности учтены).

Декомпозиция математического описания по результатам активного эксперимента

Она осуществляется по управляющим воздействиям . В этом случае разделение условий на группы производится путём выделения однородных диапазонов технологического режима по всем одновременно.

Процедура декомпозиции математического описания заключается в получении моделей диапазонов, между которых имеется существенное различие по структуре, по набору управляющих воздействий и содержит следующие этапы:

1. Методами отсеивающего эксперимента определяются наиболее информативные выходные переменные , для каждой из них выделяются существенные входные переменные и формируется связь между ними:

y_i = f ( U ₁ , …, U_n ) ,

где – вектор управляющих воздействий для i -й переменной.

2. Устанавливаются верхний и нижний пределы изменения управляющих воздействий, исходя из физических ограничений для исследуемого технологического процесса.

3. Выбираются исходная точка при движении от нижнего предела изменения управляющих воздействий и разрабатывается план активного эксперимента

, ,

где N – число опытов при постановке эксперимента, а вектор управляющих воздействий в исходном состоянии U_{j 0} = { U ₁₀ , …, U_{n 0} }

4. В результате реализации плана эксперимента Х при изменении управляющих воздействий на величину шага варьирования D U_j получают вектор экспериментальных значений выходной переменной

5. По выборке экспериментальных значений осуществляется построение математической модели в виде уравнения регрессии

,

производится оценка статистической значимости коэффициентов уравнения регрессии по результатам эксперимента с помощью критерия Стьюдента и адекватность математической модели по F-критерию Фишера.

6. Если гипотеза об адекватности модели подтверждается, то реализуются «мысленные опыты» в некоторых точках факторного пространства в направлении по , полученному при реализации плана эксперимента Х, для чего:

а) вычисляют произведения , где D U_j –шаг варьирования фактора при построении модели, и принимается за базовый тот фактор, для которого это произведение наибольшее:

б) устанавливается новый шаг варьирования для базового фактора l_d и рассматриваются соответствующие значения l_j по остальным переменным

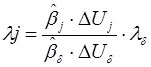
7. При реализации «мысленных опытов» определяются предсказания выходной переменной _{i пр k} в точках k в направлении , которые через два-три шага «мысленных опытов» сравниваются с экспериментальными значениями y_{i э k} :

_{i э k} - _{i пр k} = |( _{i пр} ( k +1) +( _{i пр1} - b ₀ )| £ D y_{i доп}

где _{i э k} – усреднённое значение переменой y_i по результатом параллельных опытов в точке k факторного пространства;

y_{i доп} – допустимая погрешность аппроксимации.

8. На границе адекватности модели U_{j гр} при _{i э k} - _{i пр k} > D y_{i доп}

выбирается новый уровень, реализуется план активного эксперимента и снова проводятся «мысленные опыты» в соответствии с новым базовым фактором и соответствующими шагами варьирования при движении от U_{j гр} в направлении к полученному по новому плану эксперимента Х , и так далее до верхнего предела управляющих переменных