Контрольная работа: Возраст Солнца, Звезд, Вселенной. Отличия научной картины мира от классической. Распределение солнечной энергии
В 1842 г. австрийский физик и астроном Кристиан Доплер (1803-1853) обнаружил зависимость частоты волнового импульса при движении источника волн относительно наблюдателя, названную эффектом Доплера. Многие не раз сталкивались с ним, когда слышали, как меняется звук предупреждающего свистка проносящегося мимо платформы поезда. Но эффект Доплера можно не только «слышать» но и «видеть», хотя бы в ванне или в пруду. Периодически погружая палец в воду, чтобы на поверхности образовались волны, равномерно перемещайте его в одном направлении движении. Следуя друг за другом, гребни волн будут сгущаться в направлении движения пальца и станут более разреженными с другой стороны. Значит, длина волны в направлении вперед станет меньше обычной, в направлении назад – больше.
Эффект Доплера имеет место для всех видов волн – звуковых в атмосфере, упругих в твердом теле, волн на воде, световых волн. Измерение доплеровского смещения в спектрах позволяет с большей точностью и не возмущая измерением движение и систему определить скорости движущихся объектов.
В 1848 г. французский физик Арман Физо (1819-1896) предположил использовать эффект Доплера для измерения радиальной составляющей скорости звезд по смещению спектральных линий (поэтому многие называют его эффектом Доплера-Физо). Физо обратил внимание, что в сплошном спектре движение не может вызывать заметных изменений, поэтому лучше обратиться к линейчатым спектрам, где можно измерять смещение. В 1867 г. английский астроном Уильям Хеггинс (1824-1910) обнаружил смещение водородной линии а спектре трубки Гейслера в лаборатории и заключил, что скорость звезды относительно Земли равна 66,6 км/с, а по отношению к Солнцу – 47,3 км/с[3] .
4. ДАЙТЕ ПОНЯТИЕ ВНУТРЕННЕЙ ЭНЕРГИИ. КАКИЕ ВИДЫ ВНУТРЕННЕЙ ЭНЕРГИИ ВЫ ЗНАЕТЕ? КАК ИЗМЕНЯЕТСЯ ВНУТРЕННЯЯ ЭНЕРГИЯ? В ЧЕМ СУЩНОСТЬ ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ
Внутренняя энергия - это энергия движения и взаимодействия частиц, из которых состоит вещество.
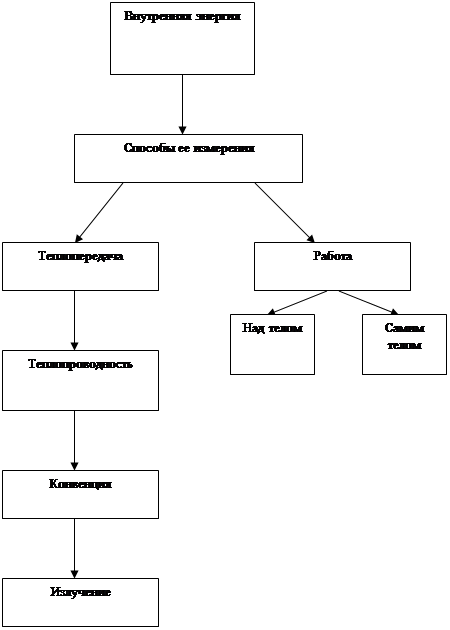 |
Внутренняя энергия любой системы складывается из энергий, входящих в нее атомов и молекул. Она представляет собой сумму кинетической энергии движения частиц (атомов, молекул или ионов), потенциальной энергии межмолекулярного взаимодействия, энергии взаимодействия электронов и ядер в молекулах и энергии, отвечающей массе покоя частиц согласно уравнению Эйнштейна. Внутренняя энергия не относится к непосредственно измеряемым величинам. На опыте удается измерить только теплоту, поглощаемую или выделяемую системой, и определить работу, связанную с переходом из одного состояния системы в другое. При любых процессах совокупность величин Q – A не зависит от пути перехода, это позволило определить изменение внутренней энергии системы с помощью уравнения
dU = d Q – d A £ TdS – dU (1)
Положительным считается такое изменение энергии, которое отвечает увеличению U в системе.
В случае равновесного процесса
d A =dA = TdS – dU (2)
При S = const (равновесный адиабатный процесс)
dA = -dU и A = U1 - U2 (3)
Интегрируя при постоянной Т уравнение (2) получаем:
A = (U1 – TS1) - (U2 – TS2) (4)
Введем обозначение
F = U – TS (5)
получим (при Т = const)
A = F1 – F2 = -D F (6)
где F – функция состояния, называемая изохорно – изотермическим потенциалом или свободной энергией системы. Переписав уравнение (5) в виде
U = F + TS
Можно рассматривать внутреннюю энергия, как энергию, состоящую из двух частей – свободной энергии F и связанной энергии TS.
Изохорный потенциал системы, находящейся при постоянных объеме и температуре, стремится уменьшиться в самопроизволных процессах.
Представим элементарную работу как сумму работы расширения и других видов работы:
d A = pdV + d A¢ (7),
где d A¢ - сумма элементарных работ всех видов, кроме работы расширения.
Из уравнений (1, 7) получаем:
d A¢ £ TdS – dU – pdV (8)
Теперь можно найти A¢ , получаемую при переходе системы из одного состояния в другое. Интегрируя это уравнение в соответствующих пределах при постоянных температуре и давлении и сгруппировав все величины, относящиеся к одному состоянию получим:
A¢ £ (U1 – TS1 + pV1) - (U2 – TS2 + pV2)
Обозначив через G выражения, стоящие в скобках правой части уравнения, которые являются функциями состояния, т. е.