Курсовая работа: Аналіз топологій

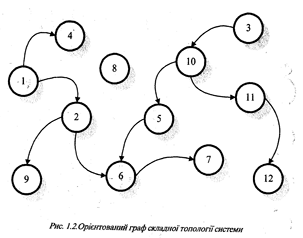
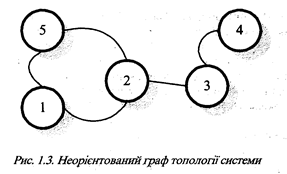
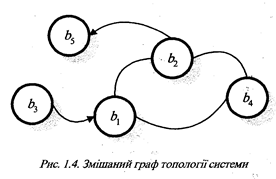
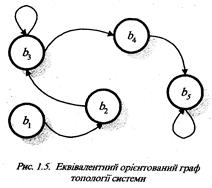
Основною перевагою графічного способу завдання топологій систем з одного боку це висока наочність безпосереднього відображення структури зв’язків між елементами системи, а з другого – достатньо розроблені в теорії графів методи їх опрацювання. Проте, графічний спосіб має й певні недоліки. По-перше, це труднощі автоматичного опрацювання графів в комп’ютерах, що пов’язані з попереднім розпізнаванням графічних образів та потреба великих обсягів пам’яті для зберігання графів. По-друге, це труднощі відображення топологій систем з великою кількістю (понад 30) елементів і як наслідок – втрата наочності. По-третє, одна і та ж топологія системи може бути задана великою кількістю еквівалентних графів із різним геометричним зображенням. Так, наприклад, топологія системи, що відображена на рис.1.1., може мати інше еквівалентне (гомоморфне) зображення, що наведене на рис.1.5., і таке не відразу може бути сприйняте як відображення однакової топології.

Власне тому графічний спосіб задання, як правило, використовується для первинного опису топологій з невеликою кількістю елементів перед введенням топологій систем в комп’ютер, а також для перевірки (верифікації) розроблених методів опрацювання при інших способах задання.

Щодо мереж Петрі, то вони застосовуються переважно для опису та моделювання систем з недетермінованою поведінкою, елемиенти яких функціонують незалежно і взаємодіють час від часу. За допомогою мереж Петрі описують як стани системи, так і дії її складових елементів. З цих міркувань застосовувати мережі Петрі для задання топологій систем недоцільно.

1.2 Матричні способи

До матричних способів відносяться: матриці (суміжності, інциденції, цикломатичні), n-мірні таблиці (масиви), n-мірні куби.

Матриця суміжності А – це квадратна матриця, що задає топологію системи і має наступний вигляд:

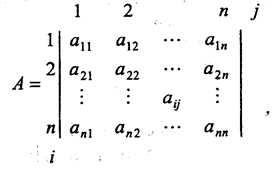
Матрицями суміжності можна задавати топології, що описуються як орієнтованими графами, так і неорієнтованими графами.

Для систем, топологія яких задається орієнтованим графом, розрізняють два типи матриці суміжності з’єднань за виходами.

Матриця суміжності з’єднань за входами – це така матриця суміжності, в якій рядки позначені елементами (номерами елементів) системи, входи яких з’єднані з виходами тих елементів системи, якими позначені стовпці матриці.

Тобто, якщо в цій матриці А_ij =1, то це означає, що вхід і-го елеметна системи з’єднаний з виходом j-го елемента.

Так, наприклад, для топології, що на рис.1.1., матриця суміжності з’єднань за входами А_І буде такою:

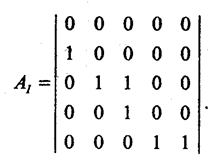
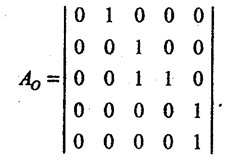
Матриця суміжності з’єднань за виходами – це така матриця суміжності, в якій рядки позначені елементами системи, якими розначені стовпчі матриці.

Тобто, якщо в такій матриці a_ij =1, то це означає, що вихід i-го елемента системи з’єднаний з входом j-го елемента.

Для тієї ж топології, що на рис.1.1, матриця суміжності з’єднань за виходами А_о буде такою:

Для задання топології систем, що описується неорієнтованим графом, застосовують тільки одну матрицю суміжності А, яка є об’єднанням матриць А_І та А_о

А= А_І А_О.

Так, наприклад, для топології, що на рис. 1.3, матриця суміжності А буде такою:

Для задання топологій систем іноді застосовують матриці інциденцій

Якщо топологія задається орієнтованим графом G=(B,E), де B={b₁ ,b₂ ,…b_n }, D={d₁ ,d₂ ,…d_m }, то матриця інциденцій для дуг S матиме такий вигляд:

Наприклад, для топології, що на рис. 1.2., матриця інциденції для дуг S буде такою:

Якщо топологія задається неорієнтованим графом G=(B,E), де B={b₁ ,b₂ ,…b_n }, D={d₁ ,d₂ ,…d_m }, то матриця інциденцій для ребер R матиме такий вигляд:

Для топології, що на рис 1.3. матриця інциденції для ребер R буде такою:

Цикломатичні матриці, яких ще називають другі матриці інциденції, можуть застосовуватися для опису топологій, що містять v незалежних циклів (контурів). Вони мають такий вигляд:

Так, наприклад, для топології, що на рис. 1.3., цикломатична матриця С, що має один незалежний контур, буде такою: