Курсовая работа: Гиперпространство

Глава 1

Существует мнение о том, что впервые понятие пространство было сформулировано в 1908г. Г.Минковским.

Наибольшую известность принесли Минковскому работы в области математической физики. В 1907–1908 гг. он дал геометрическую интерпретацию преобразований Лоренца и путем введения так называемого «пространства Минковского» (четырехмерного пространство) построил наглядную математическую модель кинематических эффектов специальной теории относительности. Геометрия Минковского, позволившая дать глубокое математическое истолкование свойств электромагнитного поля, лежит в основе современного математического аппарата теории относительности. Минковский развил также современную четырехмерную интерпретацию уравнений Максвелла, в которой их инвариантность очевидна.

Рассмотрим возможные виды пространства. Пространство в котором мы живем называется трехмерным потому, что оно имеет три измерении - высоту, ширину и глубину.

Но возникает вопрос : могут ли быть еще какие либо пространства?

Совершенно ясно, что нуль – векторного пространства быть не может, потому что это математическая точка и в ней может быть только один объект не взаимодействующий ни с чем.

Рассмотрим одномерное пространство. Это прямая линия. Предположим, что на этой линии равномерно распределены объекты – точки.

Выберем нулевую точку. На неё будут действовать, например, притягивать бесконечное количество точек слева и бесконечное количество точек справа. Поскольку сила притяжения точек не зависит от расстояния, то на нулевую точку будут действовать бесконечные силы слева и справа и разрывать её. Поэтому, такой точкой не может быть никакой материальный объект. Разрывающие силы не дадут ему образоваться, а следовательно саморазвитие не может происходить. То есть такое пространство не может существовать.

Рассмотрим двухмерное пространство. Положим опять для определённости, что объекты на поверхности расположены равномерно, объекты одинаковы и они обладают свойством притяжения. То есть опять у нас имеются бесконечные силы. Следовательно, и двумерное пространство существовать не может.

Рассмотрим теперь трёхмерное пространство. Объекты в этом пространстве уже могут существовать. Таким образом, становиться ясным, что материя может существовать как минимум в форме трёхмерного пространства, в котором имеется три координатные оси: X-ширина, Y- высота, Z-глубина.

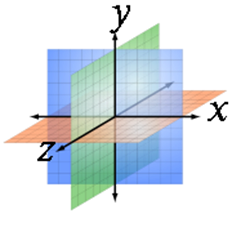
Рисунок 2

Можно поставить вопрос, а могут ли существовать пространства с координатами больше трех?

Попробуем ответить на этот вопрос, используя математическое неравенство. Пусть у нас есть четыре неизвестных x,y,z,t. В данном случае четверку чисел нужно считать точкой некоторого пространства, которое имеет четыре измерения. Значит, четырехмерное пространство может существовать.

Рассмотрим некоторые особенности четырехмерного пространства. Нарисуем на плоскости круг и представим себя в виде воображаемого существа, которое может двигаться в плоскости, но не имеет права выхода из пространства. Тогда граница круга – будет для нас непреодолимой преградой. Как показано на рисунке.

Рисунок 3

Теперь представим, что эта плоскость с нарисованным кругом помещена в трехмерное пространство. Теперь можно без труда выйти за пределы круга, просто перешагнув через окружность.

Теперь мы – существа трехмерного мира. Однако мы будем находиться внутри шара, граница которого для нас непроходима. Но если шар помещен в четырехмерное пространство, то можно без всяких усилий выйти за пределы шара.

Рисунок 4

Ничего мистического в этом нет, просто граница трехмерного шара не разбивает четырехмерного пространства на две части, хотя трехмерное пространство разбивает. Это аналогично тому, что граница круга не разбивает трехмерного пространства на две части, хотя плоскость (в которой она лежит) эта окружность разбивает.

Еще один пример: ясно, что две симметричные друг другу фигуры на плоскости нельзя совместить, если их разрешается лишь перемещать, не выводя из плоскости. Однако сидящая бабочка может сложить крылья, выводя их из горизонтальной плоскости в вертикальную.

Рисунок 5

Так же и в пространстве трех измерений нельзя совместить симметричные пространственные фигуры. Например, левую перчатку нельзя превратить в правую, хотя они являются равными геометрическими фигурами. А в пространстве четырех измерений симметричные трехмерные фигуры можно совместить подобно тому, как плоские симметричные фигуры совмещаются, если их вывести в трехмерное пространство.

Поэтому нет ничего удивительного в том, что герой рассказа Уэллса после своего путешествия в четырех мерное пространство оказался перевернутым самому себе: сердце у него оказалось справа. Это произошло потому, что, выйдя в четырехмерное пространство, он «вывернулся» в нем на другую сторону.

Координатные оси и плоскости

Точкой четырехмерного пространства называется упорядоченная четверка чисел (x,y,z,t). Поэтому в четырехмерном пространстве существуют множества точек, аналогичные координатным плоскостям трехмерного пространства. Их шесть. Каждое из них состоит из точек, у которых, как и у точек координатных плоскостей трехмерного пространства, две какие-либо координаты могут принимать любые числовые значения, а остальные две равны нулю. Каждая из этих координатных плоскостей «проходит» через координатные оси: например, плоскость yz проходит через ось y и ось z. С другой стороны, через каждую ось x проходят плоскости xy, xz и xt. Можно сказать, что ось x является пересечением этих плоскостей. Все шесть координатных плоскостей содержат общую точку (0;0;0;0) – начало координат.