Курсовая работа: Методы рационального кодирования

а для квантователя с округлением:

. ( 7)

. ( 8)

Представим квантованный сигнал в виде :

( 9)

где - ошибка или шум квантования, .

Для изучения эффектов квантования предполагают, что шум квантования обладает следующими статистическими свойствами:

1. Является стационарным белым шумом.

2. Некоррелирован со входным сигналом.

3. Распределение шума равномерное в пределах .

Для этой статистической модели определим отношение сигнал – шум квантования:

, ( 10)

где M – оператор усреднения.

Для B-разрядного квантователя можно записать соотношения:

. ( 11)

Тогда дисперсия шумов квантования при равномерном распределении ошибки равна:

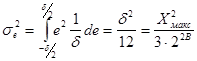. ( 12)

В случае, если , то получим выражение для отношения сигнал – шум квантования:

. ( 13)

Обычно отношение сигнал – шум задается в дБ:

. ( 14)

Из выражения ( 14) следует, что добавление одного разряда кодового слова улучшает отношение сигнал – шум квантования на 6 дБ. Выражение для отношения сигнал – шум квантования получено при предположении, что диапазон квантования используется полностью, если энергия сигнала изменится, то отношение сигнал – шум квантования уменьшится. В реальных условиях дисперсия телеметрического сигнала можно меняться на 20-30дБ. По этой причине для поддержания отношения сигнал – шум квантования на заданном уровне в случае равномерного квантования необходимо увеличивать число уровней квантования, при этом увеличивается избыточность сообщения. Желательно иметь устройство квантования, при котором отношение сигнал – шум квантования не зависит от уровня сигнала. Это достигается использованием неравномерного распределения уровней квантования.

Глава 2. Неравномерное квантование мгновенных значений

Для того чтобы относительная ошибка была постоянна при изменении дисперсии входного сигнала уровни квантования должны быть распределены по логарифмическому закону. Вместо квантования исходного сигнала можно равномерно квантовать его логарифм. В этом случае структурная схема квантователя имеет вид (рисунок 5).

Докажем, что в случае отношение сигнал – шум квантования не зависит от изменения дисперсии входного сигнала.

Выражение для квантованного логарифма входного сигнала имеет вид:

. ( 15)

Предполагается, что шумы квантования и независимы.

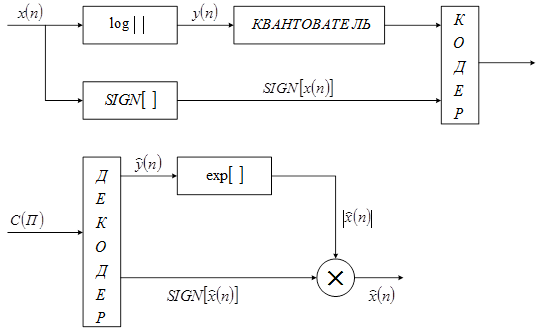
Рисунок 5

Тогда применяя обратное преобразование, получим:

. ( 16)

Если значение ошибки мало, то можно аппроксимировать экспоненту первыми членами ряда, т.е.:

( 17)

При условии, что и независимы и отношение сигнал – шум равно:

. ( 18)

Следовательно, отношение сигнал - шум квантователя не зависит от мощности сигнала и зависит только от шага квантования.

Рассмотренный выше квантователь не реализуем, т.к. динамический диапазон сигнала бесконечен и требует бесконечное число уровней квантования. Для реальных случаев число уровней квантования конечно, и характеристика компрессора может быть близка к логарифмической. На практике используемые характеристики компрессора называются и А законами компандирования.

- закон компандирования имеет следующий вид:

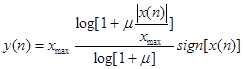. ( 19)

При малых и уровни квантования располагаются равномерно. При больших :

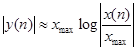( 20)

и эта характеристика близка к логарифмической.

Можно показать, что чем выше значение параметра , тем ближе характеристика компандирования к логарифмической, но тем больше проигрыш в отношении сигнал/шум. Если дисперсия входного сигнала постоянна и известна, то неравномерный квантователь проигрывает равномерному. Экспериментальные исследования показали, что двенадцатиразрядное равномерное квантование имеет такое же отношение сигнал/шум, как и в случае восьмиразрядного квантования при - законе компандирования в случае речевого сигнала (рисунок 6).

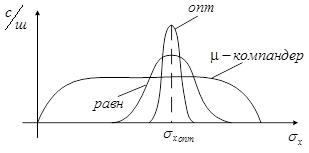
Рисунок 6

При .