Курсовая работа: Минимизация функций нескольких переменных. Метод спуска
Проведем такую же минимизацию целевой функции по переменным x, x, . . . ,xn. Дойдя до переменной xn, снова вернемся к x и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек МММ. . . , которой соответствует монотонная последовательность значений функции f(M0) f (M)f(M)Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области.
Проведем такую же минимизацию целевой функции по переменным x, x, . . . ,xn. Дойдя до переменной xn, снова вернемся к x и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М,М,М, . . . , которой соответствует монотонная последовательность значений функции
f(M0)f(M)f(M) Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области. Отметим , что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция f(x, x, ... ,xn) задана явной формулой и является дифференцируемой, то мы можем вычислить ее частные производные и использовать их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерные задачи следует решать с помощью одномерных методов
На рис.изображены линии уровня некоторой функции двух переменных u= f (х, у). Вдоль этих линий функция сохраняет постоянные значения, равные 1, 3, 5, 7, 9. Показана траектория поиска ее наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. При этом нужно ясно понимать, что рисунок служит только для иллюстрации метода.
Пусть требуется решить задачу (2):
f(x) ![]() min, х Rn. (2)
min, х Rn. (2)
В двумерном пространстве R2. Решение задачи (2) методом покоординатного спуска, иначе называемого методом Гаусса - Зейделя, производят по следующей общей схеме.
Выбирают произвольно начальную точку х(0) из области определения функции f(х). Приближения х(k) определяются соотношениями
(3):x(k+1)=x(k)+t(k)S(k) (k=0,1,2, ...),
где вектор направления спуска s(k)- это единичный вектор, совпадающий с каким-либо координатным направлением (например, если S(k) параллелен х1, то S(k)= {1,0,0,...,0}, если он параллелен x2, то S(k)={0, 1, 0, . . . ,0} и т.д.) ; величина t(k) является решением задачи одномерной минимизации:f(x(k)+ts(k)) ![]() min, t R1, (k=0,1,2, ...), и может определяться, в частности, методом сканирования. Детальная реализация общей схемы в двумерном случае R2 даеттраекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х(k), x1(k) x(k+1) (k=0, 1, 2,) . При k=0, исходя из начальнойточки х(0)=(x1(0),x2(0)), находят точку х(0)= (x1(0),x2(0)), минимума функции одной переменной f(x1,x2(0)); при этом f(x(0))f(x(0)).Затем находят точку минимума x(1) функции f (x1(0),x2) по второйкоординате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х(1). Фиксируявторую координату точки х(1), находят точку минимумах(1)= (x1(1),x2(1)), функции f(x1,x2(1)) одной переменной x(1); приэтом f(x(1))f(x(1))f(x(0)). Точку х(2) получают, минимизируя целевую функцию f(x1(1),x2), вновь по коорданате х2, фиксируя координату x1(1) ,точки x(1) , и т.д.Условием прекращения вычислительной процедуры при достижениизаданной точности может служить неравенствоx(k+1) - x(k) <
min, t R1, (k=0,1,2, ...), и может определяться, в частности, методом сканирования. Детальная реализация общей схемы в двумерном случае R2 даеттраекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х(k), x1(k) x(k+1) (k=0, 1, 2,) . При k=0, исходя из начальнойточки х(0)=(x1(0),x2(0)), находят точку х(0)= (x1(0),x2(0)), минимума функции одной переменной f(x1,x2(0)); при этом f(x(0))f(x(0)).Затем находят точку минимума x(1) функции f (x1(0),x2) по второйкоординате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х(1). Фиксируявторую координату точки х(1), находят точку минимумах(1)= (x1(1),x2(1)), функции f(x1,x2(1)) одной переменной x(1); приэтом f(x(1))f(x(1))f(x(0)). Точку х(2) получают, минимизируя целевую функцию f(x1(1),x2), вновь по коорданате х2, фиксируя координату x1(1) ,точки x(1) , и т.д.Условием прекращения вычислительной процедуры при достижениизаданной точности может служить неравенствоx(k+1) - x(k) <
Блок-схема поиска минимума функции двух переменных методом покоординатного спуска.
дискретный оптимизация спуск функция
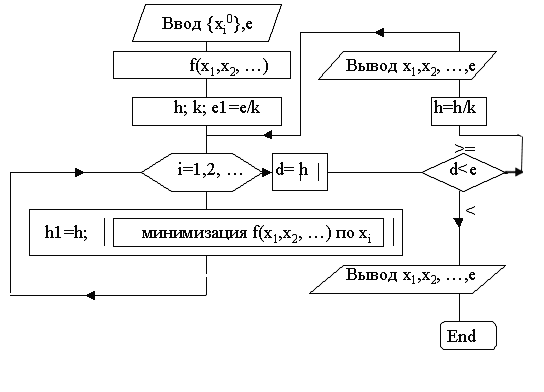
Метод градиентного спуска
Рассмотрим функцию f, считая для определенности, что она зависит от трех переменных x,y,z. Вычислим ее частные производные дf/дх, дf/ду, дf/дz и образуем с их помощью вектор, который называют градиентом функции:
gradf(x, у, z) = дf(х, у,z) /дх*i+дf( x, у, z)/ду*j+дf(x, y,z)/дг*k.
Здесь i, j, k - единичные векторы, параллельные координатным осям. Частные производные характеризуют изменение функции f по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в окрестности точки (х, у,z). Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиентаgrad (х, у,z)дf/дх (х, у,z))2 +(дf/ду( x, у, z))2+(дf/дг(x, y,z))2. определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке (х, у, z) меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются. Понятие градиента естественным образом переносится на функции любого числа переменных.
Перейдем к описанию метода градиентного спуска. Основная его идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея реализуется следующим образом.
Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции. Специальный выбор направления движения на каждом шаге позволяет надеяться на то, что в данном случае приближение к наименьшему значению функции будет более быстрым, чем в методе покоординатного спуска.
Метод градиентного спуска требует вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно.
Отметим, что при таких расчетах gi ,нельзя брать слишком малым, а значения функции нужно вычислять с достаточно высокой степенью точности, иначе при вычислении разности
f(x1, ...,xi+ gi, ..., xn) - f(x1, ..., xi, ..., xn)
f(x1, ...,xi+ gi, ..., xn) - f(x1, ..., xi- gi,..., xn)
будет допущена большая ошибка.
Первый алгоритм требует меньших затрат по сравнению со вторым (обычно затраты выражаются количеством вычислений критерия оптимальности), но позволяет получить решение менее точно, чем второй, эта погрешность зависит от величины пробного шага
Метод наискорейшего спуска
Суть метода наискорейшего спуска состоит в следующем. Как и прежде, в начальной точке определяется антиградиент минимизируемой функции. Однако теперь в направлении антиградиента делается ни один шаг, а движутся в данном направлении до тех пор, пока целевая функция убывает, достигает в некоторой точке минимума. В этой точке опять определяют антиградиент и ищут новую точку минимума целевой функции и так далее. В данном методе спуск имеет более целеустремлённый характер, производится более крупными шагами и градиент функции вычисляется в меньшем числе точек.
Описание программы:
Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций.