Курсовая работа: Оценка надежности радиоэлектронного устройства с учетом внезапных отказов путем моделирования

Пятая группа – комплексные показатели надежности, к которым относятся:

· коэффициент готовности;

· коэффициент технического использования;

· коэффициент простоя.

В данном курсовом проекте оценка надежности проводится по показателям безотказности, а именно: по вероятности безотказной работы в течение заданного времени, по среднему времени безотказной работы и гамма-процентной наработки до отказа.

1. Постановка задачи

Задачей данного курсового проекта является оценка надежности радиоэлектронного устройства (РЭУ) с учетом внезапных отказов путем моделирования на ЭВМ отказов элементов.

В результате решения необходимо определить следующие показатели надежности:

· среднее время безотказной работы;

· вероятность безотказной работы за время;

· гамма-процентную наработку до отказа.

Также необходимо выполнить аналитический расчет тех же показателей надежности и проведя сравнение его результатов с результатами моделирования ,сделать соответствующие выводы.

Для решения данной задачи необходимы следующие исходные данные:

· законы распределения времени до отказа каждого из элементов РЭУ;

· заданное время безотказной работы РЭУ;

· значение гамма.

Исходные данные для решения даны полностью и приведены в таблице 1

Таблица 1

Элемент	Законы распределения времени до отказа	Параметры закона	Приме- чание	Tз ,час	g,%
R1¼R4	Экспоненциальный	l=10-5 1/ч	5000	99
DA1	Лог. нормальный	mx =4;sx =0,3			lg
X1¼X3	Нормальный	m=5000 ч s=1000 ч

.

2. Краткое описание метода моделирования на ЭВМ отказов элементов

Областью преимущества моделирования надежности на ЭВМ являются аналитические расчеты , которые необходимы при решении практических задач по обеспечению и оценке показателей надежности РЭУ. Они часто оказываются весьма трудоемкими или ими вообще нельзя пользоваться ..

В результате решения требуемой задачи должны быть получены N реализаций РЭУ и проведена статистическая обработка выходных данных.

В данном случае необходимо смоделировать случайное время до отказа каждого элемента и получить N реализаций РЭУ . Далее необходимо найти минимальное время до отказа для каждой реализации. Затем путем статистической обработки получить среднее время безотказной работы,вероятность безотказной работы за заданное время и гамма-процентную наработку до отказа.

Достоинствами метода является :

·отсутствие необходимости испытывать реальные конструкции и технологические процессы, что делает этот метод наиболее дешевым;

·получение случайных реализаций первичных параметров;

·возможность получения любого числа реализаций РЭУ, что повышает точность оценки надежности.

3. Решение задачи на ЭВМ

Структурная схема алгоритма решения задач на ЭВМ дана в приложении.

Пояснение к алгоритму приведены в таблице 2.

Таблица 2

Номер функц. части.	Пояснение
1	Функция Z1 в которой моделируются случайные значения времени до отказа с учетом экспоненциального закона распределения по формуле
2	Функция Z2 в которой моделируются случайные значения времени до отказа с учетом нормального закона распределения по формуле
3	Функция Z3 в которой моделируются случайные значения времени до отказа с учетом логарифмического нормального закона распределения по формуле
4	Функция min которая реализует поиск элементов в j-той реализации имеющего минимальное значение времени до отказа и присвоение этого значения РЭУ, смоделированному в j-той реализации
5	Ввод количества реалиаций, количества элементов и заданного времени до отказа
6	Ввод кодов законов распределения времени до отказа: (1-экспоненциальный, 2- логарифмический нормальный, 3-нормальный)
7	Ввод данных о каждом элементе РЭУ (код закона распределения, лямбда или МО и СКО)
8	Организация цикла по переменной j, которая является счетчиком количества смоделированных РЭУ
9	Организация цикла по переменной i, которая является счетчиком количества элементов в составе РЭУ
10	Определение среднего времени безотказной работы
11	Определение вероятности безотказной работы за время tз
12	Определение гамма-процентной наработки до отказа
13	Вывод результатов моделирования

Описание используемых в программе операторов приведено в таблице 3

Таблица 3

Оператор	Значение оператора
1	Количество реализаций РЭУ
2	Количество элементов в составе РЭУ
3	Минимальное время наработки до отказа в j-той реализации РЭУ
4	МО для нормального закона распределения
5	СКО для нормального закона распределения
6	МО для логарифмического нормального закона распределения
7	СКО для логарифмического нормального закона распределения
8	Лямбда для экспоненциального закона распределения
9	Заданное время наработки до отказа
10	Среднее время безотказной работы
11	Вероятность безотказной работы за время tз
12	Количество РЭУ отказавших за время tз
13	Гамма процентная наработка до отказа

4. Аналитический расчет показателей надежности

Определение среднего времени безотказной работы РЭУ.

Для группы элементов R1-R2 с учетом экспоненциального закона распределения времени до отказа среднее время безотказной работы определяется по формуле 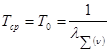1:

, (1)

где - суммарная интенсивность отказов, которая определяется по формуле 2:

, (2)