Курсовая работа: Построение трехмерной модели вазы

Для выполнения видовых преобразований должны быть заданы точка наблюдения, совпадающая с глазом, и объект. Будет удобно, если начало ее координат располагается где-то вблизи центра объекта, поскольку объект наблюдается в направлении от Е к О. Пусть точка наблюдения Е будет задана в сферических координатах f , q, rпоотношению к мировым координатам. То есть мировые координаты (точки Е) могут быть вычислены по формулам:

x_e = r sin fcos q)

y_e =r sin f sin q(2)

z_e = r cos f

Обозначения сферических координат схематически изображены на рисунке 2.

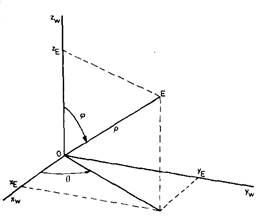
Рисунок 1 - Сферические координаты точки наблюдения Е

Видовое преобразование может быть записано в форме

[х_e y_e z_e 1]=[х_w у_w z_w 1]V, (3)

где V - матрица видового преобразования размерами 4х4.

Матрица V, полученная в процессе видового преобразования, выглядит следующим образом:

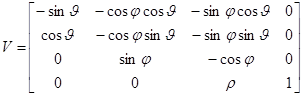(4)

Сейчас можно использовать видовые координаты х_e и у_e просто игнорируя координату z_e для получения ортогональной проекции. Каждая точка Р объекта проецируется в точку Р' проведением прямой линии из точки Р перпендикулярно плоскости, определяемой осями х и у. Эту проекцию можно также считать перспективной картинкой, которая была бы получена при удалении точки наблюдения в бесконечность. Параллельные линии остаются параллельными и на картинке, полученной при ортогональном проецировании.

Теперь для построения перспективной проекции рассмотрим непосредственно перспективное преобразование.

На рисунке 2 выбрана точка Q, видовые координаты которой равны (0, 0, d) для некоторого положительного числа d. Плоскость z = d определяет экран, который будет использоваться следующим образом. Экран — это плоскость, проходящая через точку Q и перпендикулярная оси z. Экранные координаты определяются привязкой начала к точке Q, а оси Х и Y имеют такие же направления, как оси х и у соответственно. Для каждой точки объекта Р точка изображения Р' определяется как точка пересечения прямой линии РЕ и экрана. Чтобы упростить рисунок, будем считать, что точка Р имеет нулевую у-координату. Но все последующие уравнения для вычисления ее у-координаты также пригодны и для любых других значений координаты X. На рисунке треугольники EPR и EP'Q подобны. Следовательно,

(5)

Отсюда будем иметь

(6)

X = dx/Z

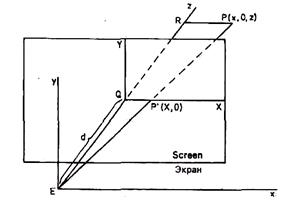
Рисунок 2 - Экран и видовые координаты

Аналогично можем получить:

Y = dy/Z. (7)

Ранее было введено предположение, что точка О начала системы мировых координат примерно совпадает с центром объекта. Поскольку ось z видовой системы координат совпадает с прямой линией ЕО, которая пересекает экран в точке Q, то начало Q системы экранных координат будет находиться в центре изображения. Если бы мы потребовали, чтобы это начало координат располагалось в нижнем левом углу экрана, а размеры экрана составляли 2с1 по горизонтали и 2с2 по вертикали, то нужно дополнить формулы вычисления X и Y:

Х = d x/z + с1

Y = d y/z + c2 (8)

2.2 Алгоритм удаления невидимых линий и поверхностей

Для изображения поверхности вазы с удалением невидимых точек в аксонометрической проекции можно воспользоваться таким свойством: видимыми являются точки с неотрицательным значением координаты Z в системе видовых координат. При этом центр видовых координат (X,Y,Z) совпадает с центром сферы, плоскость X0Y является плоскостью проецирования, а ось Z направлена на камеру (наблюдателя).