Курсовая работа: Приховані марківські процеси
![]()
![]() (2)
(2)
де a i j - це ймовірність переходу з стану S i в стан S j в даний момент часу. Оскільки ці ймовірності характеризують випадковий процес, вони мають звичайні властивості, т. е.
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
Описаний вище випадковий процес можна назвати відкритою марківською моделю, оскільки вихідний сигнал моделі - це послідовність станів реєструються в часі. Кожен стан відповідає певному (що спостерігається) події. Для того, щоб краще зрозуміти все вищесказане, розглянемо просту марківську модель погоди, у якій буде всього три стану. Передбачається, що ми один раз на день (наприклад, в опівдні), дивимося у вікно і реєструємо в журналі поточний стан погоди. Ми домовилися, що лише один із трьох нижче названих станів в день t ми записуємо в журнал:
- Стан № 1: дощ (або сніг)
- Стан № 2: хмарно, можливий дощ
- Стан № 3: ясно
Матриця ймовірностей зміни погоди A має вигляд
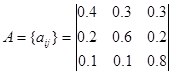
Виходячи з того, що погода в перший день (t = 1) ясна (стан 3), ми можемо задати собі питання: яка вірогідність (згідно з нашою моделі), що наступні 7 днів буде саме «зрозуміло - ясно - дощ - дощ - ясно - Хмарно, можливий дощ - ясно »? Точніше сказати, для цієї послідовності станів O, де ![]() відповідає, t=1,2,...,8, Ми хочемо на основі даної моделі визначити ймовірність спостереження послідовності O. Ця ймовірність може бути виражена (і обчислено) наступним чином
відповідає, t=1,2,...,8, Ми хочемо на основі даної моделі визначити ймовірність спостереження послідовності O. Ця ймовірність може бути виражена (і обчислено) наступним чином
![]()
![]() (4)
(4)
це ймовірність того, що початковий стан системи буде Si.
Є й інший цікаве питання, відповідь на яке нам дасть ця модель: яка вірогідність того, що модель збереже свій стан протягом рівно d днів? Ця ймовірність може бути обчислено як ймовірність спостереження такій послідовності
![]()
дає модель, в якій
![]() (5)
(5)
Величина pi (d) - це ймовірність того, що система буде перебувати в стані i рівно d раз поспіль. Відповідно є функція розподілу ймовірності для тривалості перебування системи в одному стані, яка є характеристикою збереження стану для марківських ланцюга. Знаючи величини pi (d) ми можемо обчислити середній час, протягом якого система збереже свій стан (використовуємо формулу математичного очікування):
![]() (6.1)
(6.1)
![]() (6.2)
(6.2)
Очікується, що сонячна погода швидше за все простоїть 5 днів, похмура - 2,5 дні, а от дощова погода, згідно з нашою моделі, імовірніше за все протримається 1,67 дня.
4. Існуючі шляхи вирішення задачі
У описаної марківській моделі кожній фізичній явищу відповідало певний стан моделі. Ця модель, на жаль, занадто обмежена, і їй не під силу рішення багатьох актуальних проблем. У цьому розділі ми розглянемо марківські моделі, у яких спостерігаються послідовність - це результат переходів у відповідності з позначеними ймовірностей. У даному випадку модель (прихована марківська модель) - це результат двох випадкових процесів. Перший - прихований процес - його ніяк не можна зареєструвати, але його можна охарактеризувати за допомогою іншого випадкового процесу, який надає нам набір сигналів - спостерігається послідовність. Проілюструємо цей опис на прикладі підкидання монети.
Приклад монети, яку підкидають. Ви знаходитесь в кімнаті, а за перегородкою - в іншій кімнаті - знаходиться людина, яка підкидає монету. Він не говорить, як саме він підкидає монету, а може він її взагалі лінується підкидали. Він лише говорить вам результат кожного падіння монети: орел чи решка. У цьому й полягає суть прихованого процесу (ви не знаєте, що відбувається з монетою), коли про процесі ви можете судити лише за що спостерігається послідовності
![]() ,
,
де Н - це орел, а Т - це решка.
Як же побудувати приховану марківську модель, що відповідає цій ситуації? Перше питання: скільки станів буде у моделі і що означає кожне стан такої моделі? Припустимо, що ми підкидаємо одну єдину монету, а інших у нас немає. Тоді вибір ми зупинимо на моделі з двома станами, де одне стан означає випадання орла, інше - решка. [1]
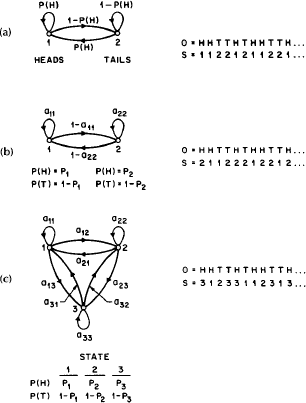
мал. 2.
Три марківські моделі, які можуть описати експеримент з монетою, що підкидається. (а) 1 монета бере участь у підкиданні, (2) 2 - монети, (3) - три монети.