1. z – располагаемое количество ресурса,

2. n – мера квантования z

3.

4.

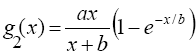
5.

Искомые параметры

1. f_N (z ) = f_N (n Δ ) - искомый максимум функции R

2. x_N (z ) – искомое оптимальное количество ресурса

МЕТОД РЕШЕНИЯ

Переходя к изложению вычислительной схемы решения задачи с применением основного функционального уравнения (1.15), предположим (а это существенно для дальнейшего изложения), что переменные задачи N i x i , ... 2, 1, , = , а также количества распределяемого ресурса как в (1.10), так и в (1.15) могут принимать только дискретные значения с некоторым выбранным шагом Δ >0. То есть имеет место:

где n Δ = z . Соответственно, функции (1.10) в рекуррентном соотношении (1.15) будут вычисляться только для указанных в (1.16) значений или, что то же самое, только для таких точек:

Указанный подход позволяет избежать процедуры интерполирования при вычислении значений , исходя из вычисленных значений f m −1( y ) в точках y = 0, Δ , 2Δ , ... , z . Действительно, для вычисления под знаком максимума в (1.15) значения − интерполирования не требуется, так как здесь с учетом (1.16) и (1.17) имеет место: .

Согласно (1.15), для вычисления вначале следует найти значения для всех значений из (1.16) с помощью соотношений (1.12)

или (1.13), которые доставляют множество всех требуемых значений

. Затем для всех (1.16) с учетом (1.15) вычисляются значения:

где.Процедура максимизации (1.18) заключается в том, чтобы вначале для каждого z ~ последовательно вычислить значения: а затем выбрать из них максимальное, то есть искомое значение ; при этом определяется и соответствующее ему оптимальное значение .

Получив множество значений для , можно приступить к вычислению функции исходя из (1.15) при m =3:

и т.д. для остальных m = 4, 5, ... , N .

Таким образом, в процессе решения уравнения (1.15) для m = 2, 3, ... , N

последовательно заполняется таблица, подобная табл. 1.1.

Таблица 1.1

Оптимальные доходы в зависимости от количества процессов

и выделенного ресурса

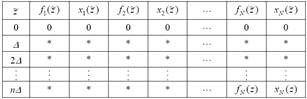
С заполнением последних двух столбцов указанной таблицы решение

задачи фактически получено. Действительно, поскольку функция по построению монотонно неубывающая по , постольку f N (z ) = f N (n Δ ) - искомый максимум функции R (1.1), а x N (z ) – искомое оптимальное количество ресурса, выделенное для N -го процесса. Стало быть, оставшееся количество ресурса, равное z − x N (z ) , должно быть распределено оптимальным образом между остальными процессами. Соответствующее решение, то есть оптимальный доход (1.10) для первых N −1 процессов, находится в столбце с заголовком − , а именно: в строке, отвечающей значению . В этой же строке в столбце с заголовком − находится величина оптимального количества ресурса, который выделяется для (N −1)-го процесса. Таким образом, перемещаясь по столбцам табл. 1.1 справа налево (это т.н. обратный ход [1, 3]), можно последовательно определить все значения , которые доставляют абсолютный максимум функции R (x 1, x 2 , ... , x N ) (1.1) в области (1.2), (1.3) для заданного количества распределяемого ресурса – z , конечно же, с учетом дополнительных ограничений (1.16), (1.17)

ОБОСНОВАНИЕ ВЫБОРА ПРОГРАММНЫХ СРЕДСТВ

Курсовая работа выполнена с помощью программы Microsoft Office Excel, одной из наиболее передовых, мощных и современных сред разработки Windows-приложений и электронных таблиц. Встроенное средство поиска решений позволяет быстро справиться с задачей о распределения ресурсов.

ОПИСАНИЕ ИНТЕРФЕЙСА ПОЛЬЗОВАТЕЛ Я

Для начала работы с программой следует задать n и z и нажать кнопку определить