Курсовая работа: Разработка программы "Формирование и проверка контрольной суммы кластеров"
Значение CRC с порождающим многочленом G(x) степени N определяется как битовая последовательность длины N, представляющая многочлен R(x), получившийся в остатке при делении многочлена P(x), представляющего входной поток бит, на многочлен G(x):
![]()
где:
R(x) — многочлен, представляющий значение CRC.
P(x) — многочлен, коэффициенты которого представляют входные данные.
G(x) — порождающий многочлен.
![]() — степень порождающего многочлена.
— степень порождающего многочлена.
Умножение xN осуществляется приписыванием N нулевых битов к входной последовательности, что улучшает качество хеширования для коротких входных последовательностей.
При делении с остатком степень многочлена-остатка строго меньше степени многочлена-делителя, то есть при делении на многочлен G(x) степени N можно получить 2N различных остатков от деления. При «правильном» выборе порождающего многочлена G(x), остатки от деления на него будут обладать нужными свойствами хеширования — хорошей перемешиваемостью и быстрым алгоритмом вычисления. Второе обеспечивается тем, что степень порождающего многочлена обычно пропорциональна длине байта или машинного слова (например 8, 16 или 32).
Операция деления на примитивный полином также эквивалентна следующей схеме:
Пусть выбран примитивный полином, задающий цикл де Брейна 0010111001011100… и блок данных 0111110, построена таблица, верхняя строка заполнена блоком данных, а нижние строки — смещения на 0,1,2 бит цикла де Брейна
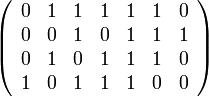
Тогда контрольная сумма будет равна операции XOR тех столбцов, над которыми в верхней строке расположена 1. В этом случае, 010 xor 101 xor 011 xor 111 xor 110 = 101 (CRC).
Алгоритм CRC32, используемый данным проектом, основан на примитивном полиноме 0xEDB88320 (зеркальное отображение полинома 0x04C11DB7) и является одним из самых распространенных методов подсчета контрольной суммы.
Еще используется криптографический алгоритм MD5.
MD5 (англ. Message Digest 5) — 128-битный алгоритм хеширования, разработанный профессором Рональдом Л. Ривестом из Массачусетского технологического института (Massachusetts Institute of Technology, MIT) в 1991 году. Предназначен для создания «отпечатков» или «дайджестов» сообщений произвольной длины. Является улучшенной в плане безопасности версией MD4.[1] Зная MD5-образ (называемый также MD5-хеш или MD5-дайджест), невозможно восстановить входное сообщение, так как одному MD5-образу могут соответствовать разные сообщения. Используется для проверки подлинности опубликованных сообщений путём сравнения дайджеста сообщения с опубликованным. Эту операцию называют «проверка хеша» (hashcheck).
На вход алгоритма поступает входной поток данных, хеш которого необходимо найти. Длина сообщения может быть любой (в том числе нулевой). Запишем длину сообщения в L. Это число целое и неотрицательное. Кратность каким-либо числам необязательна. После поступления данных идёт процесс подготовки потока к вычислениям.
Ниже приведены 5 шагов алгоритма:
Шаг 1. Выравнивание потока.
Шаг 2. Добавление длины сообщения.
Шаг 3. Инициализация буфера.
Шаг 4. Вычисление в цикле.
Шаг 5. Результат вычислений.
1.3 Выбор платформы и языка разработки приложения
Перед началом разработки был произведен анализ требований к программному обеспечению, результаты которого были преобразованы в требования к платформе разработки:
простота организации и программирования пользовательского интерфейса;
возможность работать на компьютерах с версией ОС WindowsХР и выше;
возможность работы с файловой системой Windows;
возможность работы с математическими операциями.