Курсовая работа: Технологія одержання квантових точок

Розглянемо металеву квантову точку. Енергетичне розділення рівнів біля рівня Фермі є грубо пропорційне , де - число електронів у квантовій точці. При порядку кількох еВ, та близькому до 10 атом, заборонена зона металевої квантової точки стає спостережуваною тільки при дуже низьких температурах. У випадку напівпровідникових квантових точок заборонена зона є більшою і її ефекти можуть спостерігатися при кімнатній температурі. Залежна від розмірів флуоресцентна емісія квантових точок у видимій області спектру є наглядною ілюстрацією присутності залежної від розмірів величини забороненої зони [6].

1.2 Енергетичні рівні напівпровідникової квантової точки

Нижче детальніше розглянемо нульвимірне тверде тіло. Оскільки багато квантових ефектів краще виявляються у напівпровідниках порівняно з металами, розгляд буде сфокусовано на напівпровідниковому матеріалі. Модель вільного газу електронів не включає „природу” твердого тіла. Але з макроскопічної точки зору будемо розрізняти метали, напівпровідники та ізолятори. Модель газу вільних електронів досить добре описує випадок електронів у зоні провідності металів. З іншого боку, електрони в ізолюючому матеріалі погано описуються моделлю вільних електронів. Для того, щоб розширити модель вільних електронів на напівпровідникові матеріали було введено поняття нового носія заряду – дірки. Якщо один електрон з валентної зони збуджується у зону провідності, то „порожній” електронний стан у валентній зоні називають діркою. Деякі основні властивості напівпровідникових матеріалів можуть бути описані моделлю вільних електронів і вільних дірок. Енергетичні смуги для електронів та дірок розділені забороненою зоною (енергетичною щілиною). Дисперсійні залежності для енергії електронів та дірок у напівпровіднику є параболічними у першому наближенні. Ця апроксимація справедлива тільки для електронів (дірок), що займають рівні, які знаходяться на дні зони провідності та вершині валентної зони. Кожна парабола є квазінеперервним набором електронних (діркових) станів вздовж даного напрямку у просторі. Найнижча незайнята смуга енергії та найвища зайнята смуга енергії розділені забороненою зоною , як показано на рис. 1.2. Ширина забороненої зона у масивному напівпровіднику може становити від частки еВ до декількох еВ [7].

Слід очікувати, що енергетичні дисперсійні співвідношення все ще параболічні у квантовій точці. Але, оскільки у точці можуть існувати тільки дискретні енергетичні рівні, кожна з оригінальних параболічних смуг (характерних для масивного тіла) тут фрагментується в комбінацію точок.

, (1.1)

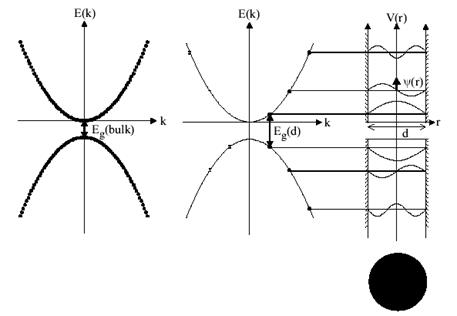
Рис. 1.2.

Вільним носіям у твердому тілі властива параболічна дисперсійна залежність ~. У напівпровіднику енергетичні смуги для вільних електронів та дірок розділені енергетичною щілиною (забороненою зоною) . У масивному напівпровіднику (рис.1.2 зліва) стани є квазінеперервними, кожна точка в енергетичних смугах представляє індивідуальний стан. У квантовій точці заряди обмежені малим об’ємом. Ця ситуація може бути описана як така, в якій носій заряду поміщено у потенціальну яму шириною та нескінченно високими стінками. Тут ширина потенціальної ями відповідає діаметру квантової точки. Єдині дозволені стани – це стани, в яких хвильова функція зникає на границях ями. Це спричинює дискретні енергетичні рівні (рис.1.2 праворуч). Енергетична заборонена зона між найнижчими можливими рівнями енергій для електронів та дірок є більшою, ніж для масивного матеріалу.

Найнижча енергія для електрону у одновимірній потенціальній ямі є тут - ширина ями. У квантовій точці носії заряду обмежені по всіх трьох напрямках, і система може бути описана як нескінченна 3-вимірна потенціальна яма. Потенціальна енергія є нулем всюди всередині ями, але є нескінченно великою на її стінках. Цю яму ще називають „ящиком”. Найпростішими формами тривимірної ями (ящика) можуть бути, наприклад, сфера або куб. Якщо форма кубічна, то рівняння Шредінгера може бути розв'язане незалежно для кожного з трансляційних ступенів свободи, і загальна енергія нульової точки є просто сумою індивідуальних нульових енергій для кожного ступеня свободи:

. (1.2)

Якщо ящик є сферою діаметром , рівняння Шредінгера може бути розв'язане шляхом введення сферичних координат та поділу рівняння на радіальну частину і частину, що містить кутовий момент. Найнижчий енергетичний рівень (з кутовим моментом = 0) тоді буде рівним

(1.3)

Ефект квантового обмеження знову значний. Більш обмежені носії заряду призводять до більшого розділення між індивідуальними рівнями енергії, а також до більших значень нульової енергії. Якщо носії поміщені у сферу діаметром , то їх нульова енергія є вищою, ніж для носіїв, поміщених у куб з ребром (, тому що така сфера має менший об’єм (), ніж куб – ().

Пара електрон-дірка може бути генерована у квантовій точці фотоіндукованим процесом або інжекцією заряду. Мінімальна енергія , що потрібна для створення електрон-діркової пари у квантовій точці, має кілька складових. Одна складова - це енергія забороненої зони масивного матеріалу . Іншою важливою складовою є енергія обмеження для носіїв, рівна . Для великих частинок (масивних: ) прямує до нуля. Можна оцінити загальну енергію обмеження для електрон-діркової пари у сферичній квантовій точці. Це є енергія нульової точки потенціальної ями, або, іншими словами, енергія стану у потенціальній ямі з найнижчою енергією. Це можна записати як

(1.4)

де - приведена маса екситону:

. (1.5)

Тут та - ефективні маси для електронів та дірок відповідно. Для того, щоб обчислити енергію, потрібну для утворення електрон-діркової пари, необхідно розглянути інший член (). Кулонівська взаємодія враховує взаємне притягання між електроном та діркою, помножене на коефіцієнт, що описує екранування носіїв кристалом. На відміну від , фізичне значення цього члену може бути зрозумілим у рамках класичної електродинаміки. Але оцінити такий член можливо тільки якщо відомі хвильові функції для електрону та дірки. Величина (сила) екрануючого коефіцієнту залежить від діелектричної постійної напівпровідника. Оцінка кулонівського члену дає

(1.6)

Цей член може бути достатньо великим, оскільки середня відстань між електроном та діркою у квантовій точці може бути мала. Можна оцінити величину забороненої зони сферичної напівпровідникової квантової точки й отримати її залежність від розміру точки:

. (1.7)

Підставивши (1.4) та (1.6) у (1.7), отримаємо:

. (1.8)

Тут підкреслено розмірну залежність кожного члена. Рівняння (1.8) є тільки першим наближенням. Багато ефектів, таких як анізотропія кристалу та спін-орбітальна взаємодія, слід розглядати у більш строгих наближеннях.

Розглянуте наближення для забороненої зони квантової точки включає два члени, які залежать від розмірів: енергія обмеження, яка змінюється з , та кулонівське притягання, яке змінюється з . Енергія обмеження завжди є позитивним членом, отже, енергія найнижчого можливого стану завжди вища по відношенню до ситуації у масивному тілі. З іншого боку, кулонівська взаємодія завжди є притяганням для системи електрон-діркова пара і таким чином зменшує енергію її утворення. Завдяки залежності від ефект квантового обмеження стає домінуючим членом для дуже малих розмірів квантової точки. Залежність забороненої зони від розмірів є корисним фактором при конструювання матеріалів з контрольованими оптичними властивостями [7].

1.3 Різноманіття квантових точок

Перед тим, як розглядати електронні та оптичні властивості квантових точок, розглянемо як практично отримуються квантові точки. Технології та методи отримання квантових точок повинні бути спроможні виробляти значну кількість зразків з таким високим контролем розміру квантової точки, форми та монодисперсності, щоб одночастинкові властивості не усереднювалися неоднорідністю зразка. До цих пір ансамблі квантових точок, вироблених з використанням найкращих технологій, все ще залежать від розмірів, але ця область розвивається дуже швидко. Різні технології та методи призводять до різних типологій квантових точок.

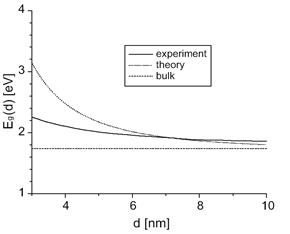
Рис. 1.3. Залежність забороненої зони від розміру для колоїдних наноточок CdSe діаметром d .