В пункте производится единиц однородного продукта. В пункте требуется единиц этого продукта.

Пусть - количество единиц продукта, перевозимого из пункта в пункт , а затраты на перевозку - материальные, - временные. Необходимо определить множество переменных (; ), удовлетворяющих условиям:

,

,

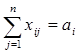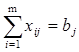и таких, что целевая функция 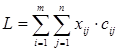достигает минимума.

· Так как во всех пунктах производства не должно остаться не вывезенного товара, необходимо условие 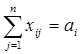, . Оно гарантирует полный вывоз продукта из всех пунктов производства

· Так как во всех пунктах потребления товара необходимо доставить согласно спросу, необходимо условие 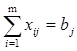, . Оно означает полное удовлетворение спроса во всех пунктах потребления.

· Количество единиц товара, перевозимого из пункта в пункт , не может быть отрицательным, следовательно, необходимо ввести условиенеотрицательности (; )

· Так как нам необходимо минимизировать суммарные материальные транспортные издержки при перевозе всего товара из пунктов производства в пункт потребления, целевая функция будет иметь вид:

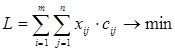
Для дооптимизации по времени необходимо использовать следующую целевую функцию:

· ,при этом необходимо учитывать, что стоимость перевозок не должна изменяться.

3. Краткие сведения о методе решения задачи

Сведение открытой модели транспортной задачи к открытой

В некоторых случаях модель транспортной задачи получается открытой, т.е. 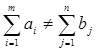возможны 2 случая:

1. 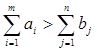, тогда вводят фиктивный пункт потребления 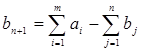, а дополнительный столбик матрицы С заполняют очень большими числами (М). После того, как решение получено, все перевозки x_{i , n +1} (), в оптимальном плане Х_k считают равными нулю.

2. 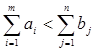, тогда вводят фиктивный пункт производства 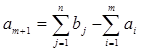, а дополнительную строку матрицы С заполняют очень большими числами (М). После того, как решение получено, все перевозки x_{m +1, j} (), в оптимальном плане Х_k считают равными нулю

Метод минимального элемента

Используют для нахождения начального опорного плана Т-задачи.

1. Элементы матрицы С нумеруют, начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х₀ :

Допустим, уже проделано k шагов метода, тогда среди незаполненной части матрицы X₀ отыскиваем элемент с минимальным порядковым номером.

Пусть элементом с минимальным порядковым номером оказался

.

Возможны три случая:

а) если , то и всю оставшуюся i-ю строку заполняют нулями, а , ;

б) если , то и весь оставшийся j-й столбец заполняют нулями, а , ;

в) если , то и оставшийся j-й столбец и i-ю строку заполняют нулями, а , .

На этом один шаг метода заканчивается.

Далее этот процесс повторяют с незаполненной частью матрицы X₀ .

Метод потенциалов:

Теорема. Если план транспортной задачи является оптимальным , то ему соответствует система из чисел , удовлетворяющих условиям для

Числа называются потенциалами соответственно го поставщика и го потребителя.

Для оптимального плана Т-задачи необходимо выполнение условий: