Лабораторная работа: Модель бензоколонки
F1(NК ) - безразмерная функциональная зависимость расходов от числа каналов.
Но, кроме показателя эффективности, существует еще критерий эффективности. В теории эффективности критерием эффективности называют правило, с помощью которого выбирается наивыгоднейший вариант структуры моделируемой системы. Если имеется несколько показателей эффективности, то критерий объединяет их в единое выражение.
В данном случае показатель один, а поэтому в качестве критерия естественно принять условие достижения максимума этого показателя. На практике это означает, что нужно перебрать несколько вариантов структуры модели при разных значениях входных параметров и установить, при каких условиях выбранный нами показатель эффективности будет достигать максимума. Для наглядности можно привести выражение для определения величины критерия эффективности. Оно будет иметь вид:
Критерий эффект. = ![]() ,
,
Где u – порядковый номер варианта расчета, принадлежащий множеству U.
Однако в самой алгоритмической модели эта формула использоваться не будет. Ею должен руководствоваться исследователь, производящий расчеты различных вариантов при переменных значениях входных параметров модели.
1. КОНЦЕПТУАЛЬНАЯ МОДЕЛЬ
Пусть имеется система массового обслуживания с переменным числом каналов NK , которое может принимать любое значение в диапазоне от одного до трех. Входной поток заявок - простейший , следовательно, время между соседними заявками имеет показательное распределение с известным математическим ожиданием (средним значением) Тз.ср .
Время обслуживания заявки в любом канале - величина случайная, имеющая показательное распределение с известным средним временем обслуживания Тобс.ср .
Все заявки однородны и независимы.
Правило (дисциплина) обслуживания состоит в том, что очередная заявка поступает в тот канал, который раньше других освободился. Если время ожидания начала обслуживания превышает заданную величину Тож. max , то заявка покидает систему необслуженной. Период функционирования СМО характеризуется величиной Tкон .
Таким образом, входными характеристиками модели являются: число каналов NK ,среднее время между соседними заявками Tз.ср , среднее время обслуживания заявки Тобс.ср , максимально допустимое время ожидания Тож. m ах ,период работы системы Ткон. , число случайных реализаций моделируемого процесса Np .
Выходной характеристикой модели является среднее число обслуженных заявок Nобс.ср
Выбор показателя и критерия эффективности
В качестве показателя эффективности работы системы целесообразно выбрать среднюю прибыль, определяемую по формуле
| Сc р = С1 * Nобс.ср – С2 (NK ), | (1) |
где С1 - чистая прибыль, полученная в результате обслуживания однойзаявки;
С2 (NK ) - издержки обслуживания всех заявок, зависящие от числа каналов.
Разделим обе части равенства (1) на величину С1 . Получим следующее выражение для расчета показателя эффективности:
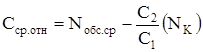 , , | (2) |
где Cc р.отн - средняя относительная прибыль.
Величину С2 /С1 (отношение издержек обслуживания к чистой прибыли, полученной в результате обслуживания одной заявки) будем рассматривать как функцию числа каналов.
Предположим, что возможными вариантами этой функциональной зависимости являются: а - линейная зависимость; б - возрастающая зависимость с положительной 2-й производной и в - возрастающая зависимость с отрицательной 2-й производной (рис. 1).
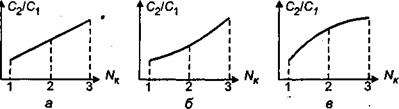
Рис.1.Зависимости отношения С2 /С1 , от NК : а - первый вариант; б - второй вариант; в - третий вариант
Выберем второй вариант. Примем в качестве конкретной зависимости издержек обслуживания от числа каналов следующую функцию:
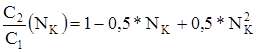 . . | (3) |
Итак, для расчета показателя эффективности будем использовать зависимости (2) и (3).
В качестве критерия выбора наивыгоднейшей структуры СМО примем оптимальное число каналов, обеспечивающее максимум средней относительной прибыли:
| (4) |
где NK * - наивыгоднейшее число каналов.
2. СХЕМЫ АЛГОРИТМОВ МОДЕЛИ
В качестве языка программирования для разработки компьютерной модели рассматриваемого процесса выбран VisualBasic 5.0.
Общий вид (макет) стартовой формы показан на рис. 2. Видно, что она включает ряд объектов управления, среди которых имеются три командные кнопки: «Расчет», «Очистка» и «Выход». Это обстоятельство определяет структуру алгоритма процедур обработки прерываний, показанную на рис. 3.
После нажатия кнопки «Start» активизируется стартовая форма. С этого момента программа находится в режиме ожидания действий пользователя.
Цифрой 1 (рис.3) обозначено действие, заключающееся в корректировке исходных данных. Необходимые изменения вносятся в соответствующие текстовые поля.
Цифрой 2 обозначено действие, заключающееся в нажатии (с помощью мыши) кнопки «Расчет». В процедуре, связанной с этой кнопкой, оператор 3 осуществляет перевод исходных данных из символьной формы в числовую. Затем оператор 4 обращается к модулю общего назначения «Model2». Схема алгоритма этого модуля приведена на рис. 4.
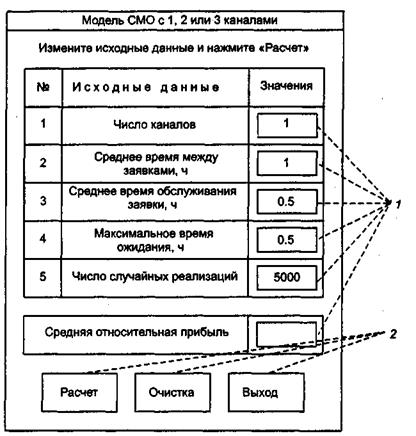
Рис. 2.Макет стартовой формы:
1 - текстовые поля; 2 - командные кнопки