Лабораторная работа: Оцінка трудомісткості алгоритму

Таблиця 2

n0=	1	n0=	1
n1=	0.8n0	n1=	0.8
n2=	1n1+0.2 n2+0.8 n5	n2=	5
n3=	0.8n2	n3=	4
n4=	0.3n3	n4=	1.2
n5=	0.7n3+1n4	n5=	4
n6=	0.2n5	n6=	0.8
n7=	0.2 n0+1n6	n7=	1

6. Знаходження середньої кількості процесорних операцій за допомогою програмиMicrosoftExcelпоказана на рис.4.

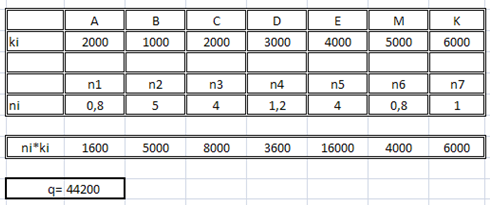
Рисунок 4

7. Знаходження кількості звернень до файлів та довжин за допомогою програми MicrosoftExcelзображено на рис.5.

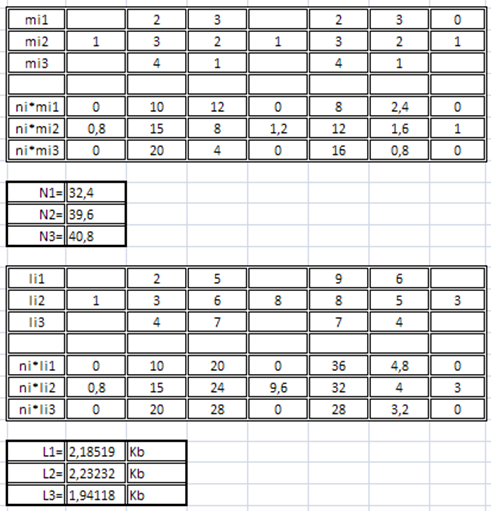
Рисунок 5

Частина 2 . Компіляція програми

Операційна система Linuxмає багато вбудованих компіляторів, практично під кожну мову програмування високого рівня. Два найбільш поширені компілятори – це gccта g++ для мов програмування С та С++ відповідно. В даній лабораторній роботі я використовував компілятор g++, з допомогою якого скомпілював програму, що обчислює числа Фібоначчі. Ця програма складається з двох файлів lab.cpp та fib.h. Перший містить головну функцію програми і слугує для вводу виводу чисел. Другий проводить математичні операції з числами. Результат виконання програми об’єднується і записується в один об’єктний файл lab1. Щоб зібрати всі файли в один, потрібно використати ключ –о, наприклад: g++ lab.cppfib.h –olab1. Виконуємо отриманий файл за допомогою команди ./lab1 .

Нижче наведено лістинг програми та скріншот, який показує результат виконання.

Лістинг 2.1 lab.cpp

#include <iostream>

#include "fib.h"

using namespace std;

int main()

{

long n;

cout<<"Enter the fibonacci number:"; cin>>n;

cout<<"The "<<n<<" number of fibonacci is:"<<fibonacci(n)<<endl;

return 0;

}

Лістинг 2.2 fib.h

long fibonacci ( long n)

{

if ( n == 0)

{

return 0;

}

else if ( n == 1 )