Научная работа: Основы аэронавтики

2. Расчеты Архимеда

2.1 Закон Архимеда

1) На тело, погруженное в жидкость (газ), действует выталкивающая сила, равная весу вытесненной им жидкости.

FА = ρgV

где р - плотность жидкости (газа), g - ускорения свободного падения, а V - объем погруженного тела ( или часть объема тела, находящаяся ниже поверхности). Выталкивающая сила, называемая также архимедовой силой, равна по модулю и противоположна по направлению силе тяжести, действовавшей на вытесненный телом объем жидкости (газа), и приложена к центру тяжести этого объема.

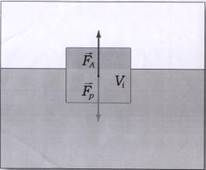
Следует заметь, что тело должно быть полностью окружено жидкостью. Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна. 2) Мы не можем точно проследить логику рассуждений Архимеда. За древностью лет много информации, к сожаленью, утеряно, но попробуем мысленно перенестись в 287 – 212гг до н.э. и воссоздать картину размышлений великого греческого ученого изложенную в сочинении «О плавающих телах».

Сочинение " О плавающих телах " исследователи относят к числу самых поздних, а некоторые считают его последним научным трудом Архимеда. Это сочинение состоит из двух книг. В первой книге Архимед, излагает: тела, равнотяжелые с жидкостью, будучи опущены в эту жидкость, погружаются так, что никакая из часть не выступает над поверхностью жидкости и она не будет двигаться вниз. Подробно разбирает вопросы, связанные с погружением твердых тел в жидкость, и формулирует закон, до сих пор приводимый в любом школьном учебнике. И здесь подход к проблеме тот же: на основание опытных наблюдений Архимед строит модель жидкости, с помощью которых получает ряд следствий, обосновывая их строгими геометрическими доказательствами. Во второй книге: тело более легкое, чем жидкость, будучи опущено в эту жидкость, не погружается целиком, но некоторая часть его остается над поверхностью жидкости ; Тело более тяжелое, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела. Он рассматривает принцип работы ареометра и условие равновесия в жидкости тел, имеющих форму сегмента параболоида. Выводы Архимеда представляли практический интерес судостроения. 3) Рассмотрим вывод закона Архимеда с точки зрения математики.

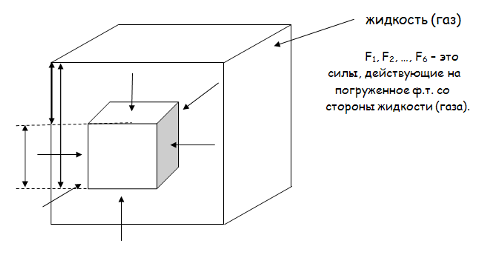
На все шесть граней физического тела действует со стороны жидкости (газа) гидростатическое давление р = рgh, так как боковые грани находятся на одинаковых глубинах (h3 = h4= h5 = h6) и ρ=const, g = const, то ρ3 = ρ4 = ρ5 = ρ6. С другой стороны ρ = S . Так как мы рассматриваем физическое тело кубической формы, то S1 = S2 = S3 = S4 = S5 = S6 и, следовательно, F3 = F4 = F5 = F6 и эти силы компенсируют действия друг друга (F3 + F4 + F5 + F6 = 0). Теперь рассмотрим F1 и F2. Так как h1 < h2 , то ρ = ρgh при ρ = const и g = const , ρ1 < ρ2. Так как ρ = S => F = ρS при S1 = S2 , то F1 < F2 Определяя равнодействующую силу F1 и F2 , найдем , что R = F1 + F2 , так как F1 F2 , то R = F2 - F1 , = 0. Это сила была названа выталкивающая и позже в честь Архимеда, названа FА - Архимедова сила Вычислим FА : FА = F2 - F1 , так как

F = ρS, то FА = ρ2S2 - ρ1S1 ; ( S1 = S2 = S ); FА = ρ2S - ρ1S = S(ρ2 - ρ1).

Учитывая, что ρ = ρgh, получаем:

FА = S(ρ2g2h2 - ρ1g1h1) - g1 = g2 = g = const ,

так как это ускорение свободного падения (g≈9,8) - ρ1 = ρ2 = ρ = const , так как физическое тело погруженное в однородную жидкость. Тогда :

FА = S(ρgh2 - ρgh1) = Sρg(h2-h1)

Из рисунка видно, что h2 - h1 = h ф.т., тогда

FА = Sρgh ф.т.

Из курса математики следует:

Sh ф.т. = V ф.т

то

FА = ρgV ф.т. 4)

Продолжим рассуждения, начатое в 3 пункте. Из курса динамики известно, что P = mg для случая если U = 0, а = 0, так как

mж = ρжVж

то

FА = ρж(г)V ф.т. g

Если взять столько жидкости (газа), чтобы наблюдалось равенство Vф.т. = Vж(г) . (Рассматриваем жидкость (газ), взятую в объеме погруженного физического тела) , тогда:

FА = Pж(г) (при Vф.т. = Vж(г)).

2.2 Условия плавания тел

1. Если FА › mg, то физическое тело поднимается вверх.