Реферат: Деревья и их свойства (частный вид графов)

2 . Единственная простая цепь между x0 и любой другой вершиной x графа G' является путем в орграфе G, идущим из вершины x0 в вершину x.

На рис. 3 изображено ориентированное дерево.

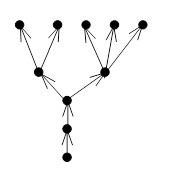
Рис. 3

В неориентированном графе G(X, E) вершина x называется концевой или висячей, если d(x) = 1, т.е. если этой вершине инцидентно единственное ребро e. Это ребро также называется концевым или висячим. С висячими вершинами связана следующая теорема.

Теорема 2. В любом дереве G(X, E) с p ³ 2 вершинами имеется не менее двух концевых вершин.

Доказательство. Пусть q – число ребер дерева G. В силу теоремы 1 p = q + 1. Кроме того, из теоремы 1.1 имеем

.

Таким образом, получаем

. (1)

Предположим, что x0 – единственная концевая вершина в дереве G. Тогда d(x0) = 1, d(x) ³ 2, если x¹x0. Отсюда

. (2)

Неравенство (2) противоречит (1), поэтому либо концевых вершин нет, либо их по крайней мере две. Если концевых вершин в G нет, то d(x) ³ 2 для всех xÎX. Тогда

. (3)

Неравенство (3) тоже противоречит (1). Отсюда следует, что концевых вершин в G две или больше. Теорема доказана.

Важным является вопрос о том, сколько существует деревьев с заданным числом вершин. Для деревьев с помеченными вершинами (например пронумерованными) или для помеченных деревьев ответ на этот вопрос дает следующая теорема.

Теорема 3. (А. Кэли, 1897 г.). Число помеченных деревьев с p вершинами равно pp-2.

Доказательство. Пусть G(X, E) – дерево с p помеченными вершинами. Для простоты предположим, что вершины пронумерованы в произвольном порядке числами 1, 2, …, p. Рассмотрим способ, позволяющий однозначно закодировать дерево G.

В соответствии с теоремой 2 дерево G имеет концевые вершины. Пусть x1 – первая концевая вершина в последовательности 1, 2, …, p и пусть e1 = (x1, y1) – соответствующее концевое ребро. Удалим из дерева вершину x1 и ребро e1. Получим новое дерево G1 с числом вершин p - 1. Найдем теперь пер­­вую концевую вершину x2 дерева G1 в последовательности вершин 1, 2, … …, p из множества {1, 2, …, p }\{x1}, далее возьмем концевое ребро e2 = (x2, y2) и удалим из G1 x2 и e2. Эту процедуру последовательно повторяем. Через (p - 2) шага остается дерево из двух вершин xp-1, yp-1 и одного ребра ep-1 = (xp-1, yp-1). Рассмотрим последовательность вершин

s(G) = {y1, y2, …, yp-2}.

Очевидно, что по данному дереву последовательность строится однозначно. Покажем теперь, что по данной последовательности вершин s (G) дерево G можно восстановить однозначно. В последовательности 1, 2, …, p существуют вершины, не принадлежащие s (G). Выберем первую из них x1 и построим ребро e1 = (x1, y1). Затем удалим x1 из последовательности 1, 2, …, n и y1 удалим из s(G). Аналогичным образом построим ребро e2 = (x2, y2). Продолжая этот процесс, мы однозначно восстановим дерево G. Рассмотрим пример.

Построение кода	Восстановление
s(G)	s(G) и список вершин
(2,6,5,5,6) 1,2,3,4,5,6,7 (2)
(6,5,5,6) 2,3,4,5,6,7 (2,6)
(5,5,6) 3,4,5,6,7 (2,6,5)
(5,6) 4,5,6,7 (2,6,5,5)
(6) 5,6,7 (2,6,5,5,6)

Рассмотренный пример позволяет отметить следующие две особенности:

1 В списке s(G) вершины могут повторяться.

2 . При восстановлении дерева последнее ребро соединяет вершину yp-2 и оставшуюся в списке 1, 2, …, p вершину не равную yp-2.

Итак, существует взаимно однозначное соответствие между множеством помеченных деревьев с p вершинами и множеством последовательностей вершин s(G). Число таких последовательностей равно, очевидно, pp-2, что и требовалось доказать.

Отметим, что среди pp-2 помеченных деревьев с p вершинами могут быть и изоморфные.

Определение 3. Подграф G1(X1, E1) неориентированного графа G(X, E) называется каркасом, или остовным деревом графа G, если G1 – дерево и X = X1.

Теорема 4. Граф G(X, E) тогда и только тогда обладает каркасом, когда он связен.

Доказательство. Необходимость этого очевидна. Докажем достаточность. Пусть G(X, E) – связный граф. Выясним, есть ли в графе G такое ребро, удаление которого не нарушает связности графа G. Если таких ребер нет, то граф есть дерево в соответствии с теоремой 1. Если же такое ребро, например e, существует, то выбросим его и придем к графу G1(X, E\{e}). Затем указанную процедуру проделываем с графом G1 и т.д. Через конечное число шагов будет построен, очевидно, каркас графа G. Теорема доказана.