Реферат: Детекторная система ЭКТ

; ; ; , (4)

здесь R₀ – сопротивление резистора в цепи обратной связи сумматора.

Наиболее простой способ определения весовых коэффициентов состоит в линейной аппроксимации их зависимости от координат. Рассмотрим, как это делается на примере группы ФЭУ, расположенных на оси X матрицы, состоящей из 19 ФЭУ (см. рис.3). Эта группа изображена на рис 5 Коэффициент а⁺ изменяется слева направо от нуля до единицы, а коэффициент а^– наоборот – от единицы до нуля. Это значит, что левый крайний ФЭУ (3) не вносит никакого вклада в координатный сигнал Х⁺ , а правый крайний (4) – в Х^– . Весовой коэффициент ФЭУ, расположенного в центре (1), равен 0,12 Поэтому его вклады в сигналы Х⁺ и Х^– будут одинаковыми и при их вычитании они компенсируются.

Рисунок 5 К расчету весовых коэффициентов координатной матрицы.

Сопротивления резисторов и определяются по формулам (3). На рис. 5 их графики имеют вид гипербол, зеркально отраженных относительно оси симметрии. При этом сопротивления для ФЭУ 13 и для ФЭУ 19 будут равны R₀ , а для центрального ФЭУ все четыре весовых резистора будут иметь одинаковые сопротивления 2R₀ . Сопротивления и соответственно для ФЭУ 19 и 13 равны бесконечности, т.е. просто отсутствуют. Весовые сопротивления для ФЭУ 4 и 7 будут равны соответственно 4R₀ и 4/3R₀ , или 1,333R₀ . Из этого простого примера видно, что для координатной матрицы нужно брать высокоточные спротивления (не менее 0,1%).

Для оптимизации сопротивлений резисторной матрицы можно воспользоваться критериями минимума нелинейности пространственной зависимости координатных сигналов или минимума неоднородности изображения. Сущность первого метода состоит в минимизации суммы квадратов отклонений координатных сигналов от истинных координат сцинтилляций, вычисленных в нескольких тестовых точках, равномерно покрывающих площадь детектора. График коэффициентов а⁺ , найденных этим методом, показан на рис.5 тонкой линией.

Резисторные матрицы подключаются к входам сумматоров, которые выполняются на быстродействующих операционных усилителях. Особенность работы сумматоров состоит в большой частоте и относительно малой скважности импульсов. Это приводит к появлению существенной постоянной составляющей на разделительных и паразитных емкостях, которая вызывает смещение нуля входного операционного усилителя сумматора.

??????? 6. ???????? ???????????? ????????

Кроме того, необходимо учитывать, что для исследований могут применяться РН с разными энергиями g-квантов. При этом выходной сигнал сумматора нужно изменять соответствующим образом, т.е. нормировать. Схема сумматора, учитывающая эти особенности, приведена на рис.6.

На резисторную матрицу через разделительные конденсаторы поступают положительные импульсы от предварительных усилителей ФЭУ. Эти импульсы заряжают конденсаторы, и на них появляется отрицательное (по отношению к общей точке) смещение. Оно будет тем больше, чем выше частота импульсов. В результате может сильно вырасти (вплоть до насыщения ОУ) постоянная составляющая выходного напряжения сумматора. Чтобы скомпенсировать смещение, сумматор охватывают нелинейной отрицательной ОС. Для этого его выходной сигнал еще раз инвертируют и подают на вход прецизионного выпрямителя (DA2, VD1, VD2). Он пропускает только положительные импульсы и при этом их инвертирует. Цепочка R3, C1 выделяет из них постоянную составляющую U_CР , которая и компенсирует смещение, вызываемое средним уровнем входных импульсов (базовый уровень). Для нормирования выходного сигнала по энергии применяемого изотопа применен перемножающий ЦАП, играющий роль аттенюатора. На вход опорного напряжения (Ref) подают аналоговый сигнал, а на цифровые входы – код изотопа. Он зависит от энергии изотопа: чем больше энергия, тем меньше код.

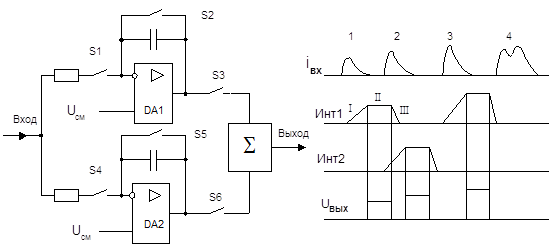
Выходные импульсы сумматоров еще нельзя непосредственно использовать для дальнейшей обработки, так как их информационные параметры недостаточно определенны. Более объективную информацию дает интегрирование этих импульсов: площадь импульса пропорциональна энергии. Кроме того, при этом исходные импульсы сложной формы можно преобразовать в импульсы стандартной прямоугольной формы. Принцип интегрирования координатных и энергетических импульсов поясняет рис.7.

??????? 7. ?????????? ???????????? ? ?????????????? ????????

Поскольку сцинтилляции имеют случайный характер (пуассоновское распределение), то интервалы между импульсами имеют большой разброс. Они могут быть настолько малыми, что интегратор может оказаться не готовым к интегрированию очередного импульса. В схеме рис.7 эта проблема решается применением двух интеграторов, включенных параллельно. Если к приходу очередного импульса один из интеграторов оказывается занятым, то функция интегрирования передается другому. Выходные сигналы интеграторов объединяются сумматором.

Работа каждого интегратора состоит из трех стадий. Допустим, что работает первый интегратор. На стадии I замкнут ключ S1, а S2 и S3 разомкнуты – производится интегрирование входного сигнала. На стадии II замкнут ключ S3, а S1 и S2 разомкнуты – стадия хранения; при этом на выходе сумматора возникает прямоугольный импульс. На стадии III ключи S1 и S3 разомкнуты, а S2 замыкается – происходит сброс интегратора. К моменту появления импульса 2 первый интегратор еще находится в стадии хранения, поэтому функция интегрирования передается второму интегратору. Работой устройства управляет специальная схема, формирующая импульсные последовательности с учетом амплитудно-временных параметров входных сигналов.

Еще одной проблемой, которую приходится решать в этом узле, представляет наложение импульсов (на рис.7 это импульс 4). Такие импульсы сливаются в один, но вызваны они могут быть вспышками с разными координатами. Поэтому наложенный импульс несет не информацию, а дезинформацию, и его лучше вовсе исключить из общей последовательности. Схема управления делает это на основе амплитудно-временных признаков.

Выходные сигналы координатных интеграторов поступают в корректор энергетической зависимости координатных сигналов. Это устройство является одним из самых оригинальных аналоговых устройств гамма-томографа ГКС-301Т и его преемника – томографа ОФЭКТ. Поэтому оно заслуживает более подробного рассмотрения. Как уже отмечалось, вместо энергетического сигнала Z в нем в качестве сигнала-делителя используются суммы составляющих координатных сигналов X = X₊ – X_– и Y = Y₊ – Y_–

Рассмотрим вначале общую задачу аналогового деления двух сигналов. Она может быть решена различными способами. Один из них показан на рис.8. Делитель состоит из двух логарифмических преобразователей (логарифматоров) на операционных усилителях DA1, DA2 и транзисторах VT1.1, VT1.2. Эти транзисторы так же, как и транзисторы VT2.1 и VT2.2, представляют собой элементы микросхемы (транзисторной сборки). Поэтому они практически идентичны, что обеспечивает симметрию схемы и малый дрейф.

Рисунок 8. Делитель аналоговых сигналов.

Действие логарифматоров основано на нелинейной зависимости между током эмиттера и напряжением эмиттер-база. Эта зависимость может быть представлена в виде двух эквивалентных формул

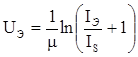или , (5)

где I_S – обратный ток (насыщения) эмиттерного перехода; m = 1/mj_т ; j_т = кТ/e – тепловой потенциал; m – коэффициент (m = 1 – 2 )

Так как в дальнейшем в основном будем оперировать коллекторными токами, и учитывая, что они практически равны эмиттерным токам, в формулах (5) заменим I_Э на I_К . Кроме того, учитывая, что единица в скобках этих формул обычно намного меньше первых слагаемых, запишем их в виде

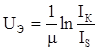и (6)

Далее, говоря о токе транзистора, будем подразумевать его коллекторный ток.

Выходное напряжение U₁ микросхемы DA1 равно U_Э транзистора VT1.1. Ток этого транзистора равен сумме входных токов, вызываемых сигналами X = X⁺ – X^– и Z = X⁺ + X^– :

, где n – коэффициент (n > 1).

Используя вторую формулу из (127), получим

.

На второй логарифматор сигнал Х подается через инвертор. Поэтому выходное напряжение микросхемы DA2 будет определяться формулой

.