Реферат: Фазовый и частотный методы измерения дальности
(tд max << Тм), то нарушением линейности можно пренебречь и считать формулу (2) справедливой для любого закона частотной модуляции. Соотношение tд max << Тм является также условием однозначного отсчета дальности.
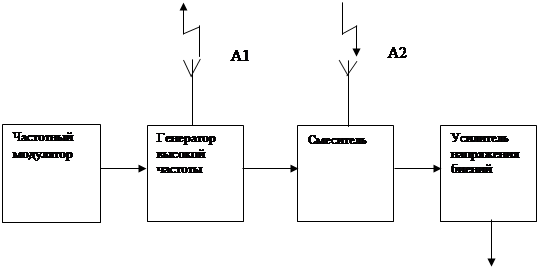
Реализация частотного метода дальнометрии. По способу обработки сигналов неследящие частотные измерители делятся на корреляционные, с фильтровой обработкой и с корреляционно-фильтровой. Третий вариант, наиболее простой в осуществлении, представлен функциональной схемой дальномера (Рис.2) и временными диаграммами (Рис.3).
Передающее устройство состоит из генератора высокой частоты, модулятора, изменяющего частоту генерируемых колебаний по пилообразному или синусоидальному закону, и передающей антенны А1. Первым каскадом приемника является смеситель, с которого начинается Корреляционно-фильтровая обработка: в смесителе перемножаются отраженный сигнал uотр(t), который подводится от приемной антенны А2, с опорным сигналом uпр(t), который подводится по короткому кабелю от передатчика; накопление энергии происходит в RC-фильтрах нижних частот, следующих за перемножителем. Как во всяком смесителе, перемножение происходит в нелинейном элементе и в результате образуются составляющие суммарной и разностной частот отраженного и опорного (прямого) сигналов. Сигнал с частотой биений пропускается к усилителю низкой частоты, а составляющие суммарных частот подавляются фильтрами нижних частот смесителя.
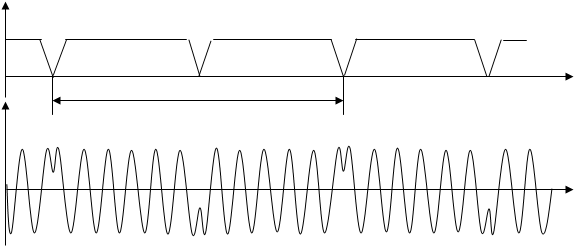
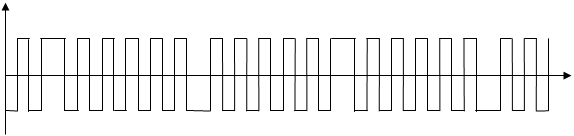
Как показывает временная диаграмма напряжения биений uб (Рис.3), когда частота его Fб отклоняется от своего основного значения, синусоидальность этого напряжения нарушается. Двухсторонний ограничитель амплитуды, следящий за усилителем низкой частоты, преобразует полученное несинусоидальное напряжение с периодом Тм в прямоугольные колебания uогр. Так называемый счетчик нулей определяет частоту биений Fб по числу переходов через нуль, которые совершают положительные перепады этих колебаний за период модуляции Тм. Переходы отмечены точками на временной диаграмме. Если число их Nm умножить на частоту модуляции Fм, то получится частота дальности, которую фиксирует индикатор
Fб= NmFм (3)
Если счетчик аналоговый (Рис.3), то выходное напряжение uсч постоянное, а если счетчик цифровой, то работа его сводится к подсчету эталонных импульсов, пропорциональных, как и напряжение uсч, частоте дальности. Очевидно, что индикатор при таком счетчике должен показывать дальность цели в цифровой форме.
В связи с тем, что счетчики подсчитывают число полных биений, показания частотного дальномера изменяются скачками. Наименьшая Функциональная схема частотного радиодальномера с корреляционно-фильтровой обработкой сигналов
 | |
 | |
Рис.2
Временные диаграммы частоты биений и напряжений в измерителе частотного радиодальномера с корреляционно-фильтровой обработкой сигналов
 | ||
 | ||
 | ||
Рис.3
дальность Дmin, которую способен измерить дальномер, соответствует одному полному биению за период модуляции (Nm=1). Согласно (3) это означает, что Fб=Fм, а из (2) следует, что Fм=4ΔfmFмДmin/с. Отсюда находим минимальную дальность, измеряемую частотным дальномером:
Дmin=с/4Δfm (4)
Следующие показания дальномера будут соответствовать уже двум (Nm=2; Fб=2Fм), трем (Fб=3Fм) и т.д. полным биениям за один период модуляции. Значит, имеется ошибка дискретности измерения дальности, равная скачку
ΔД=с/4Δfm (5)
При измерении дальности нескольких целей измеритель должен содержать спектроанализатор, рассчитанный на последовательный или параллельный анализ частот биений.
Последовательный анализ производится плавным изменением частоты гетеродина приемника или оптимального фильтра, следующего за смесителем. Это требует больших затрат времени и связано с неполным использованием энергии отраженного сигнала во время перестройки.
Многоканальный параллельный спектроанализатор (Рис.4) состоит из узкополосных фильтров Ф1,Ф2,Ф3,…, детекторов Д1, Д2, Д3, Д4, …. и неоновых лампочек ЛН1, ЛН2, ЛН3, ЛН4, …. . Полосы пропускания фильтров примыкают друг к другу и охватывают весь диапазон измеряемых частот дальности. По номерам загорающихся лампочек можно судить о том, к какому участку (каналу) дальности относится каждая наблюдаемая цель.
Ясно, что чем уже полоса пропускания фильтра ΔFф, тем выше разрешающая способность по дальности и тем меньше возможные расхождения между истиной и указываемой индикатором дальностью цели. Этому же способствует увеличение частоты модуляции и девиации частоты.
Сказанное подтверждается формулами среднеквадратической ошибки σд и потенциальной разрешающей способности ΔДmin п частотного дальномера:
![]() (6)
(6)
![]() (7)
(7)
Функциональная схема многоканального параллельного спектроанализатора
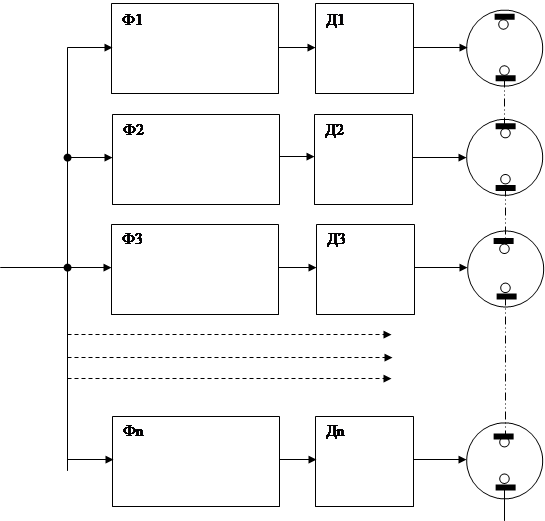 |
Рис.4
2.Фазовые методы дальнометрии.
Общие сведения. Измерение дальности фазовыми методами заключается в измерении приращения фазы гармонического колебания масштабной частоты за время запаздывания отраженного сигнала:
Δφ=Ωмtд=2πFм·Д/с=4πД/λм (8)
Частота Fм и длина волны λм=с/Fм называются масштабными потому, что от них зависит масштаб шкалы дальности, т.е. коэффициент пропорциональности между измеряемым фазовым сдвигом Δφ и дальностью цели Д.
Через фазовые интервалы Δφ=2π гармоническое колебание, а с ним и показания фазометра повторяются. Отсюда согласно формуле (8) максимальный предел однозначно измеряемой дальности
Додн=λм/2 (9)
Наиболее простым по устройству был бы фазовый радиодальномер с излучением колебаний только одной – несущей частоты fо. Но тогда масштабная частота Fм=fо и длина волны λм=λо=с/fо, а так как РЛС обычно работают на УКВ, то это ограничило бы однозначно измеряемую дальность несколькими метрами (Додн= λм/2).
Вместе с тем масштабная частота влияет на точность определения дальности. Действительно, из формулы (9) дальность Д=сΔφ/4πFм=λмΔφ/4π, и если фазометр измеряет Δφ со среднеквадратической ошибкой σΔφ, то дальность определяется со среднеквадратической ошибкой
σд =сσΔφ/4πFм=λмσΔφ/4π (10)
Шумы препятствуют точному определению фазового сдвига и увеличением отношения сигнал/шум qо ошибка σΔφп уменьшается: σΔφп=1/![]() [рад]. С учетом этого из формулы (10) находим потенциальную среднеквадратическую ошибку измерения дальности фазовыми методами:
[рад]. С учетом этого из формулы (10) находим потенциальную среднеквадратическую ошибку измерения дальности фазовыми методами:
σдп=сσΔφп/4πFм=с/4πFм![]() =λм/4π
=λм/4π![]() (11)
(11)
Как видно, всем фазовым дальномерам присуще противоречие: увеличение масштабной частоты способствует повышению точности измерений, но уменьшает предел однозначно измеряемой дальности. Рассмотрим, как разрешается это противоречие в двух применяемых на практике фазовых методах.
Фазовый радиодальномер с модуляцией несущей. Передающая антенна излучает радиоволны несущей частоты fо, модулированные по амплитуде гармоническими колебаниями низкой частоты F, а сравнение фаз излучаемого и отраженного сигналов производится на частоте огибающей Fм этих сигналов. Пропорционально уменьшению масштабной частоты от fо до Fм=F (увеличению масштабной длины волны λм=с/F) возрастает однозначно измеряемая дальность Додн. Например, при частоте модуляции F=300 Гц длина волны λм=3·10![]() /300=10
/300=10![]() м и Додн=λм/2=10
м и Додн=λм/2=10![]() /2=5·10
/2=5·10![]() м=500 км.
м=500 км.
В передатчике дальномера (Рис.5,6) колебания генератора высокой частоты модулируются по амплитуде колебаниями генератора масштабной частоты. Отраженные от цели АМ колебания усиливаются и демодулируются амплитудным детектором. Следовательно, выходное напряжение приемника uпрм имеет частоту, равную масштабной Ωм=2πFм, но отличается по фазе от напряжения uм на Ωмtд. Этот фазовый сдвиг измеряется фазометром.
На функциональной схеме показан неследящий измеритель фазы с дискретным счетом дальности. Измерение сводится к счету числа эталонных импульсов Nэт, генерируемых за время запаздывания сигнала tд. Очевидно, что период следования этих импульсов Тэт должен быть строго стабильным и существенно меньше запаздывания сигнала tд даже при минимальной дальности цели.
Сравниваемые по фазе синусоидальные напряжения uм и uпрм преобразуются амплитудными ограничителями в прямоугольные колебания uом и uопрм, которые затем перемножаются, чтобы получить колебания отрицательной полярности в течение времени tд и положительной полярности в остальную часть полупериода модуляции. Каскад совпадения имеет два входа: на один от генератора отрицательных эталонных импульсов поступают колебания uэт, а на другой от перемножителя-колебания uом и uопрм. Так как те и другие совпадают по знаку только в интервалы времени tд, то эталонные импульсы uэт проходят к счетчику пачками Nэт=tд/Tэт и цифровой счетчик указывает дальность цели пропорционально числу Nэт:
Д=ctд/2=сNэтТэт/2=сNэт/2Fэт. (12)
Ошибка дискретности измерителя соответствует периоду эталонных импульсов:
ΔДдкр=![]() сТэт/2=
сТэт/2=![]() с/2Fэт (13)
с/2Fэт (13)
Увеличение частоты Fэт уменьшает ошибку ΔДдкр, но усложняет реализацию счета импульсов. При Fэт=10![]() Гц имеем ΔДдкр=
Гц имеем ΔДдкр=![]() 3·10
3·10![]() /2·10
/2·10![]() =
=![]() 15 м.
15 м.