Реферат: Искусственное пополнение эксплуатационных запасов подземных вод

Наиболее распространенная технология - инфильтрационные бассейны прямоугольной формы, 200-400 м на 20-50 м; площадь дна 5 - 10 тыс. кв.м; глубина 2 - 3 м (рис.6.8). В бассейне поддерживается постоянный уровень; для этого через систему затворов подается такой расход "сырой" воды, чтобы компенсировать расход инфильтрации через дно бассейна. Зная подаваемый объем воды за время можно рассчитать интенсивность инфильтрации из бассейна:

где - площадь дна бассейна.

В зависимости от состава пород в зоне аэрации величина инфильтрации может составлять 0.2 - 3 м/сут, т.е. при площади дна бассейна 5 тыс. кв.м расход инфильтрации может составлять 1 - 15 тыс. куб.м/сут.

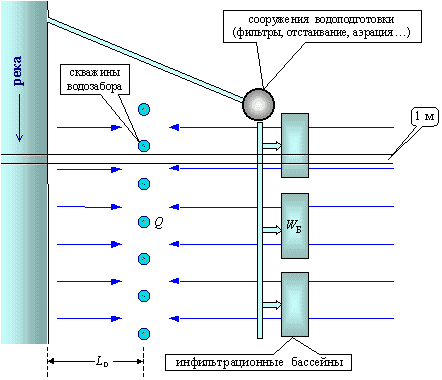Рис.6.8. Принципиальная схема системы искусственного пополнения с помощью инфильтрационных бассейнов

Основная проблема эксплуатации инфильтрационных бассейнов - неизбежная кольматация отложений в дне бассейна, несмотря на специальную водоподготовку (снижение мутности до 5-20 мг/л). Выделяют три механизма кольматации:

механическая - образование поверхностного наилка на дне бассейна и задержка взвешенных частиц в порах придонного слоя (0.1 - 0.5 м) отложений зоны аэрации;

физико-химическая - за счет выпадения осадка в виде карбонатов и сульфатов кальция, гидроокислов железа и марганца и др.;

биологическая - за счет деятельности бактерий, развития планктона (сине-зеленых водорослей).

В связи с развитием процессов кольматации скорость инфильтрации из бассейна довольно быстро снижается (рис.6.9) и через некоторое время работа бассейна становится малоэффективной. Длительность так называемого фильтроцикла составляет в разных условиях 3 - 6 месяцев (иногда более), после чего производится чистка бассейна путем механического удаления закольматированных донных отложений с последующей подсыпкой фильтрующей гравийно-песчаной смеси. На период чистки в работу запускается резервный бассейн.

С целью более длительного сохранения фильтрующей способности донных отложений производится высадка в бассейнах водной растительности (камыш, рагоз и др.). При этом дополнительно улучшается очистка воды; так, например, камыш не только разрыхляет грунт дна, повышая его фильтрационные свойства, но и поглощает фенолы, хлор и др.

Рис.6.9. Изменение скорости инфильтрации из бассейнов во времени

В связи с существованием слабопроницаемой пленки инфильтрация из бассейнов почти всегда имеет характер "дождевания" (аналогично фильтрации из несовершенной реки при отрыве уровня от подошвы экрана). Поэтому в расчетных схемах инфильтрационные бассейны следует рассматривать как граничные элементы с условием 2-го рода (заданный расход инфильтрации - с реальной динамикой во времени, либо в осредненных по времени величинах).

Интересный и практически важный вопрос - оценка эффективности ИПЗ, которую логично оценивать с помощью специального коэффициента:

,

где - соответственно дебит водозабора без пополнения и при наличии пополнения; - расход воды, поступающий из бассейнов в пласт.

Характерная схема водозаборного сооружения - линейный ряд скважин вдоль реки с параллельной системой инфильтрационных бассейнов. Если рассматривать линейную структуру потока (по ленте тока шириной 1 м - рис.6.8), то

где - погонный водоотбор из эквивалентной траншеи с уровнем ; - погонный расход инфильтрации из бассейнов.

Балансовая структура стационарного водоотбора без пополнения (рис.6.10, 11).

Два варианта взаиморасположения водозабора и инфильтрационных бассейнов

1 вариант - инфильтрационные бассейны расположены за линией водозаборного ряда (рис.6.10).

Можно уверенно считать, что при подъеме уровней под бассейном величина естественного расхода практически не изменится, так как область питания находится достаточно далеко и относительно небольшое повышение уровней не повлияет на величину инфильтрационного питания. Величина привлечения из реки тоже не изменится (), так как сохраняются отметки Hг и Hс (Hл). Поэтому при наличии ИПЗ:

Рис.6.10. Вариант 1

2 вариант - инфильтрационные бассейны размещены между рекой и водозаборным рядом.

На рис.6.11 видно, что в этих условиях расход также не меняется, но величина привлечения из реки совершенно очевидно изменится в связи с подъемом уровней между рекой и водозабором ().

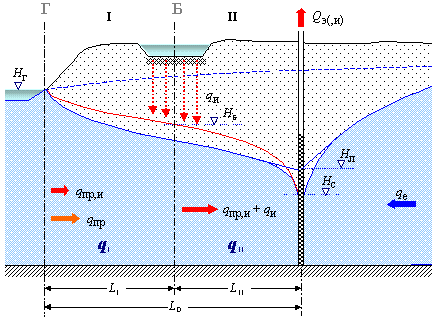Рис.6.11. Вариант 2

Поэтому уравнение баланса будет иметь вид . Чтобы оценить реальные значения χ в этих условиях, сделаем некоторые преобразования.

Во-первых, на разрезе видно, что .

Во-вторых, запишем выражения для всех расходов по формулам для линейной структуры потока (при этом используем схему с независимой проводимостью, хотя реально это, скорее всего, не так; однако, для студентов не должно составить затруднения переписать нижеследующие построения для схемы однородного по вертикали потока).