Реферат: Исследование синхронного сдвигающего регистра на JK-триггере
Ki = y · Qi-3 + y · Qi+3
_ ___ _ ___
Ji+Ki = y · Qi+3 + y · Qi-3 + y · Qi-3 + y · Qi+3 = 1
 | |||
 |  | ||
 | |||
Переводим Ji = y · Qi +3 · y · Qi -3
 |
__ _ ___
Ki = y · Qi-3 · y · Qi+3
_
Ki = Ji
Схема имеет вид:
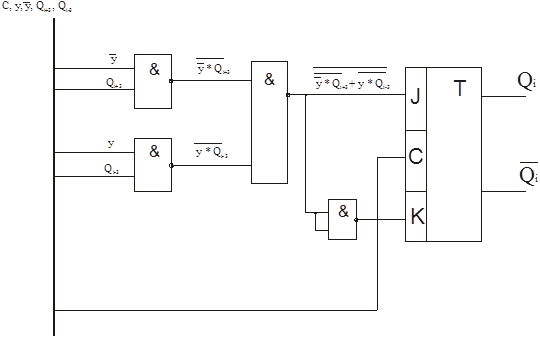
Чтобы получить выражение, описывающее логику формирования сигналов на входе триггера, используем уравнение: Ji = y · Qi +3 + y · Qi -3 , где i = 1..8, причем если результат подстановки i окажется меньше или равным нулю, то к результату следует прибавить максимальное (в данном случае 8) количество разрядов в проектируемом регистре, если же результат окажется больше максимального количества разрядов (т.е. 8), то из него следует вычесть это максимальное число.
_
J1 = y·Q4+ y·Q6
J2 = y·Q5+ y·Q7
J3 = y·Q6+ y·Q8
J4 = y·Q7 + y·Q1
J5 = y·Q8+ y·Q2
J6 = y·Q1+ y·Q3
J7 = y·Q2+ y·Q4
J8 = y·Q3 + y·Q5
Схема сдвигающего регистра, построенного по полученным выражениям выглядит следующим образом:
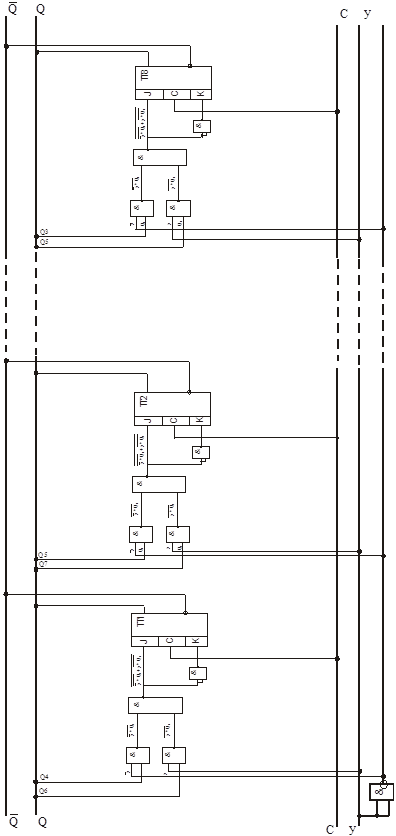
2.Синтез триггерного устройства.
Исходными данными для проектирования являются функция внешних переходов триггера и условия переключения выходного сигнала триггера по отношению к синхросигналу С.
Таблица внешних переходов JK-триггера:
| K | J | Q | Qn+1 | jQi |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | a |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | b |
| 1 | 1 | 0 | X | X |
| 1 | 1 | 1 | X | X |
Определим ограничения на изменения входных сигналов С, J, K.
- при изменении С, сигналы J и K не должны меняться
- при С=1, сигналы J и K не могут изменяться одновременно
- при С=0, никакие ограничения на изменение J и K не накладываются
- одновременное изменение С, J и K не допустимо.
Описание работы триггера представим в виде таблицы внутренних состояний JK-триггера:
| № состояния | Состояния входных сигналов C, J, K | Q | |||||||
| 000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 | 0 | |
| 1 | (1) | 2 | 3 | 4 | - | - | - | 8 | 0 |
| 2 | 1 | (2) | 3 | 4 | - | - | 7 | - | 0 |
| 3 | 1 | 2 | (3) | 4 | - | 6 | - | - | 0 |
| 4 | 1 | 2 | 3 | (4) | 5 | - | - | - | 0 |
| 5 | - | - | - | 4 | (5) | - | - | - | 0 |
| 6 | - | - | 3 | - | - | (6) | - | - | 0 |
| 7 | 1 | 2 | - | - | - | - | (7) | - | 0 |
| 8 | 1 | - | - | - | - | - | - | (8) | 0 |
| 9 | (9) | 10 | 11 | 12 | - | - | - | 16 | 1 |
| 10 | 9 | (10) | 11 | 12 | - | - | 15 | - | 1 |
| 11 | 9 | 10 | (11) | 12 | - | 14 | - | - | 1 |
| 12 | 9 | 10 | 11 | (12) | 13 | - | - | - | 1 |
| 13 | - | - | - | 12 | (13) | - | - | - | 1 |
| 14 | - | - | 3 | - | - | (14) | - | - | 1 |
| 15 | - | 10 | - | - | - | - | (15) | - | 1 |
| 16 | 1 | - | - | - | - | - | - | (16) | 1 |