Реферат: К вопросу об использовании компьютерного тестирования в обучении высшей математике

Рис. 1

Возможности программной оболочки позволяют создавать экранные формы с включением в них, наряду с формулами и графиками, различных графических объектов (рисунков, объектов WordArt и т.д.), что значительно повышает визуальный эффект и соответственно интерес студентов к тестированию.

Несмотря на большой перечень возможностей и преимуществ данной оболочки, при проектировании методики использования этого программного продукта в учебном процессе, необходимо учесть и ряд его недостатков, таких как:

недостаточно разработанная система защиты тестирующей программы;

невозможность использования банка заданий и, как следствие, невозможность создания многовариантных тестовых заданий.

Последнее обстоятельство представляется нам достаточно существенным недостатком в процессе оценивания знаний по высшей математике. Поэтому использовать данную разработку в качестве эффективного средства текущего и итогового контроля не представляется возможным. Но, в то же время, процедура того же тематического контроля, проводимая в форме КТ, может быть рассмотрена как элемент самоконтроля и обучения, и нести тем самым большую учебно-педагогическую нагрузку.

Рассмотрим подробно содержание одного из тематических тестов.

Тест № 1. Комплексные числа

Тест содержит 12 теоретических и 5 практических вопросов, типов A – D. Цель теста – обнаружение у учащегося основных теоретических знаний, практических умений и навыков по вопросам:

понятие модуля и аргумента комплексного числа;

различные формы комплексного числа;

действия над комплексными числами.

Оптимальное время тестирования (установленное в процессе диагностического исследования) 40 минут. Приведем экранные формы некоторых заданий теста.

Теоретический вопрос типа А (экранная форма на Рис. 2):

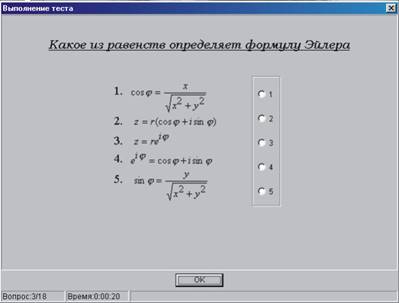
Рис. 2

Учащемуся необходимо определить формулу Эйлера из пяти предложенных. Ответить следует «флажком» на соответствующем номере, после чего нажатием клавиши «ОК» совершается переход к следующему вопросу.

При необходимости, переход от одного вопроса к другому совершается посредством «результативного» окна, в котором дается информация о правильности ответа.

Практический вопрос типа А (экранная форма на Рис. 3).

Ответ на этот вопрос предполагает предварительное решение с использованием формулы Муавра для дробного показателя.

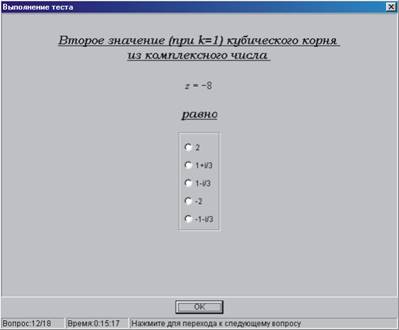
Рис. 3

Вопрос типа C, теоретический в данном случае (Рис. 4):

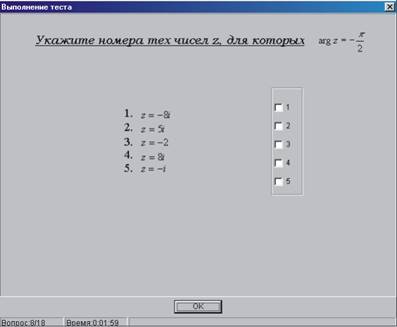
Рис. 4

Ответить на данный вопрос следует установкой двух (номера 1 и 5) «флажков». Проверяются знания основных понятий о комплексных числах.

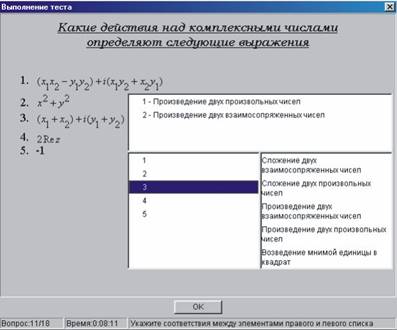
Рис. 5

Вопрос типа D – теоретический вопрос на соответствие (Рис. 5).