Реферат: Классификация и виды потоков событий
9.) математическое ожидание промежутка z между вызовами:
![]() ,
,
10.) дисперсия промежутка z между вызовами:
![]() ,
,
11.) среднеквадратическое отклонение промежутка t:
![]() ,
,
12.) математическое ожидание числа вызовов за промежуток t:
![]() ,
,
13.) дисперсия числа вызовов за промежуток t:
![]() ,
,
14.) совпадение за промежуток для простейшего потока на практике удобно использовать при проверке соответствия реального потока модели простейшего потока времени между вызовами подчинено показательному закону и является достаточным условием существования простейшего потока.
Показательно распределения широко применяется в теории телетраффика, теории массового обслуживания благодаря свойству:
если известно, что случайный промежуток распределенный по показательному закону длился уже некоторое время ![]() , то закон распределения оставшейся части промежутка также будет показательным и с тем же параметром и не будет зависеть от
, то закон распределения оставшейся части промежутка также будет показательным и с тем же параметром и не будет зависеть от ![]() .
.
Потоки с ограниченным последействием
Под потоком с ограниченным последействием понимается поток вызовов, у которого последовательность промежутков времени между вызовами ![]() представляют последовательность взаимно независимых случайных величин, имеющих любые функции распределения. У потока с ограниченным последействием вероятность поступления нового вызова в промежутке
представляют последовательность взаимно независимых случайных величин, имеющих любые функции распределения. У потока с ограниченным последействием вероятность поступления нового вызова в промежутке ![]() зависит только от расположения этого промежутка по отношению к моменту поступления последнего вызова и не зависит от времени поступления всех остальных.
зависит только от расположения этого промежутка по отношению к моменту поступления последнего вызова и не зависит от времени поступления всех остальных.

Для этих потоков в момент поступления вызова будущее не зависит от прошлого и все последствие ограничено величиной промежутка между вызовами.
Особое место среди потоков с ограниченным последействием занимают рекуррентные потоки, у которых все промежутки между вызовами, включая первый имеют одинаковой распределение ![]() при
при ![]() и рекуррентные потоки с запаздыванием, у которых только первый промежуток имеет распределение, отличное от других и они задаются двумя функциями распределения
и рекуррентные потоки с запаздыванием, у которых только первый промежуток имеет распределение, отличное от других и они задаются двумя функциями распределения ![]() и
и ![]() при
при ![]() . Функция
. Функция ![]() характеризует распределение промежутка времени от прозвольно выбранного начала отсчета
характеризует распределение промежутка времени от прозвольно выбранного начала отсчета ![]() до момента поступления первого вызова.
до момента поступления первого вызова.
К потокам с ограниченным последействием относятся потоки Пальма, Эрланга, Бернулли.
Поток Пальма
Поток Пальма – это стационарный ординарный рекуррентный поток с запаздываниями или стационарный ординарный поток с ограниченным последействием.
Задается поток Пальма условной вероятностью ![]() отсутствия вызовов в промежутке длительностью
отсутствия вызовов в промежутке длительностью ![]() , если в начальный момент этого промежутка поступил вызов:
, если в начальный момент этого промежутка поступил вызов:
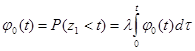
![]()
![]() ,
,
где ![]() - функция Пальма-Хинчина, определяющая вероятность отсутствия вызовов на интервале длинной
- функция Пальма-Хинчина, определяющая вероятность отсутствия вызовов на интервале длинной ![]() при условии, что в начале интервала имелся вызов;
при условии, что в начале интервала имелся вызов;
![]() - параметр потока Пальма или интенсивность потока и
- параметр потока Пальма или интенсивность потока и
![]()
Модель потока Пальма – описываемый поток необслуженных коммутационной системой вызовов.
Некоторые свойства потока Пальма:
1) объединение нескольких независимых потоков Пальма не дает вновь поток Пальма;
2) разделение одного потока Пальма на ![]() направлений с вероятностью
направлений с вероятностью ![]() поступления вызовов в
поступления вызовов в ![]() -ом направлении дает поток Пальма в каждом их этих направлений.
-ом направлении дает поток Пальма в каждом их этих направлений.
3)
Поток Эрланга
Поток Эрланга образуется в результате просеивания исходного простейшего потока вызовов.
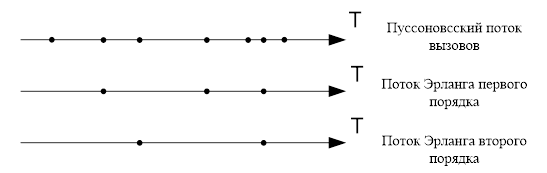
Поток Эрланга ![]() -го порядка образуется путем отбрасывания
-го порядка образуется путем отбрасывания ![]() -го вызова и сохранениея
-го вызова и сохранениея ![]() вызова.
вызова.
Основные характерные свойства потока Эрланга:
1) промежутки между вызовами независимы между собой и одинаково распределены, поскольку они получаются суммированием одинакового числа независимых промежутков исходного простейшего потока;
2) закон распределения с плотностью ![]() :
:
![]()
![]() - плотность распределения величины промежутка между вызовами
- плотность распределения величины промежутка между вызовами ![]() .
.
3) параметр потока ![]() -го порядка:
-го порядка:
![]()
4) математическое ожидание величины ![]() (промежутка между вызовами)
(промежутка между вызовами)
![]()
5) дисперсия
![]()
Поток Бернулли
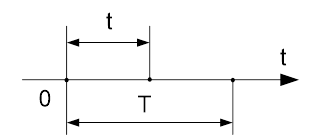
Поток Бернулли – это ординарный поток с ограниченным последействием для которого на заданном конечном интервале [0, T ) случайным образом поступает фиксированное (равное n) число вызовов. Моменты поступления вызовов независимы и равномерно распределены в интервале [0, T ) , т.е. для этих вызовов выполнено свойство случайности.
? Или ?
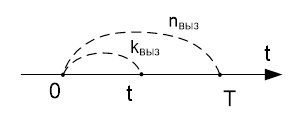
Основные характерные свойства потока Бернулли:
1) Вероятность поступления ровно k вызовов в любые промежутки [0, t ) , где t < T определяется:
![]() ,
,
где ![]() -число сочетаний из n по k :
-число сочетаний из n по k :
![]() ,
,
n - количество вызовов на промежутке [0, T )
2) Параметр потока Бернулли
![]()