Реферат: Линейные блоковые коды

где I_r - единичная матрица; - прямоугольная матрица в транспонированном виде матрицы R_k,r из порождающей матрицы.

Пример. Проверочная матрица (5,3) - кода

Основные свойства линейных кодов

1. Произведение любого кодового слова на транспонированную проверочную матрицу дает нулевой вектор размерности (n-k)

Пример. для кода (5,3)

2. Произведение некоторого кодового слова, т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается S_i (x)

3. Между порождающей и проверочной матрицами в систематическом виде существует однозначное соответствие, а именно:

4. Кодовое расстояние d₀ (n,k) - кода равно минимальному числу линейно зависимых столбцов проверочной матрицы

Пример.

для кода (5,3):

для кода (5,2):

5. Произведение информационного слова на порождающую матрицу дает кодовое слово кода

Пример. для кода (5,3)

6. Два кода называются эквивалентными, если их порождающие матрицы отличаются перестановкой координат, т.е. порождающие матрицы получаются одна за другой перестановкой столбцов и элементарных операций над строками.

7. Кодовое расстояние любого линейного (n,k) - кода удовлетворяет неравенству (граница Сингтона). Линейный (n,k) - код, удовлетворяющий равенству, называется кодом с максимальным расстоянием.

Стандартное расположение группового кода

Стандартное расположение группового кода представляет разложение множества всех возможных n-элементных слов, представляющих собой группу, на смежные классы по подгруппе из 2^k кодовых слов, составляющих (n,k)-код (см. таблицу 2).

Таблица 2
				

Образующие или лидеры смежных классов выбираются таким образом, чтобы в их состав вошли наиболее вероятные образцы ошибок в кодовом слове, т.е. образцы ошибок с наименьшим весом.

Пример. Код (5,3) имеет матрицы

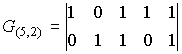и

а стандартное расположение имеет вид,

00000	10111	01101	11010
00001	10110	01100	11011
00010	10101	01111	11000
00100	10011	01001	11110
01000	11111	00101	10010
10000	00111	11101	01010
00011	10100	01110	11001
10001	00110	11100	01011

Этот код имеет d₀ =3. Он гарантирует исправление одиночных ошибок, конфигурация которых дана в первом столбце.

Процедура исправления ошибок следующая. Принятое кодовое слово анализируют и определяют, в каком столбце оно находится, а затем в качестве исправленного кодового слова берут слово, находящееся в верхней строке.