Реферат: Линейные списки. Стек. Дек. Очередь

Список с использованием указателей (linked list) – список, в котором каждый элемент содержит указатель на следующий элемент списка.

Линейный список (linear list) — это множество, состоящее из узлов , структурные свойства которого по сути ограничиваются лишь линейным (одномерным) относительным положением узлов, т. е. теми условиями, что если , то является первым узлом; если , то k-му узлу предшествует и за ним следует ; является последним узлом.

Операции, которые мы имеем право выполнять с линейными списками, включают, например, следующие:

1. Получить доступ к k -му узлу списка, чтобы проанализировать и/или изменить содержимое его полей.

2. Включить новый узел непосредственно перед k-ым узлом.

3. Исключить k-й узел.

4. Объединить два (или более) линейных списка в один список.

5. Разбить линейный список на два (или более) списка.

6. Сделать копию линейного списка.

7. Определить количество узлов в списке.

8. Выполнить сортировку узлов списка в возрастающем порядке по некоторым полям в узлах.

9. Найти в списке узел с заданным значением в некотором поле.

Специальные случаи k=1 и k=n в операциях (1), (2) и (3) особо выделяются, поскольку в линейном списке проще получить доступ к первому и последнему элементам, чем к произвольному элементу.

В машинных приложениях редко требуются все девять из перечисленных выше операций в самом общем виде. Мы увидим, что имеется много способов представления линейных списков в зависимости от класса операций, которые необходимо выполнять наиболее часто. По-видимому, трудно спроектировать единственный метод представления для линейных списков, при котором все эти операции выполняются эффективно; например, сравнительно трудно эффективно реализовать доступ к k-му узлу в длинном списке для произвольного k, если в то же время мы включаем и исключаем элементы в середине списка. Следовательно, мы будем различать типы линейных списков по главным операциям, которые с ними выполняются.

Очень часто встречаются линейные списки, в которых включение, исключение или доступ к значениям почти всегда производятся в первом или последнем узлах, и мы дадим им специальные названия:

Многие люди поняли важность стеков и очередей и дали другие названия этим структурам; стек называли пуш-даун (push-down) списком, реверсивной памятью, гнездовой памятью, магазином, списком типа LIFO ("last-in-first-out" — "последним включается — первым исключается") и даже употребляется такой термин, как список йо-йо! Очередь иногда называют — циклической памятью или списком типа FIFO ("first-in-first-out" — "первым включается — первым исключается"). В течение многих лет бухгалтеры использовали термины LIFO и FIFO как названия методов при составлении прейскурантов. Еще один термин "архив" применялся к декам с ограниченным выходом, а деки с ограниченным в ходом называли "перечнями", или "реестрами". Такое разнообразие названий интересно само по себе, П оскольку оно свидетельствует о важности этих понятий. Слова "стек" и "очередь" постепенно становятся стандартными терминами; из всех других словосочетаний, перечисленных выше, лишь "пуш-даун список" остается еще довольно распространенным, особенно в теории автоматов.

При описании алгоритмов, использующих такие структуры , принята специальная терминология; так, мы помещаем элемент на верх стека или снимаем верхний элемент. Вниз у стека находится наименее доступный элемент, и он не удаляется до тех пор, пока не будут исключены все другие элементы. Часто говорят, что элемент опускается (push down) в стек или что стек поднимается (pop up), если исключается верхний элемент. Эта терминология берет свое начало от "стеков" закусок, которые можно встретить в кафетериях, или по аналогии с колодами карт в некоторых перфораторных устройствах. Краткость слов "опустить" и "поднять" имеет свое преимущество, но эти термины ошибочно предполагают движение всего списка в памяти машины. Физически, однако, ничего не опускается; элементы просто добавляются сверху, как п ри стоговании сена или при укладке кипы коробок. В применении к очередям мы говорим о начале и конце очереди; объекты встают в конец очереди и удаляются в момент, когда наконец достигают ее начала. Говоря о деках, мы указываем левый и правый концы. Понятие верха, низа, начала и конца применимо иногда и к декам, если они используются как стеки или очереди. Не существует, однако, каких-либо стандартных соглашений отно­сительно того, где должен быть верх, начало и конец: слева или справа. Таким образом, мы находим, что в наших алгоритмах применимо богатое разнообразие описательных слов: "сверху — вниз" — для стеков, "слева — направо" — для деков и "ожидание в очереди" —для очередей.

Однонаправленный и двунаправленный список – это линейный список, в котором все исключения и добавления происходят в любом месте списка.

???????????????? ?????? ?????????? ?? ???????????????? ?????? ?????? ??????. ?? ???? ? ???????????????? ?????? ????? ???????????? ?????? ? ????? ??????????? (?? ?????? ? ?????), ? ??????????????? ? ? ?????. ?? ??????? ??? ?????: ?????? ???????????????? ??????, ? ????? ???????????????

?? ??????? ????? ??? ??????????? ? ????????? ??????? ?? ???????????????? ??????. ??? ?????????? ?????? ???????? (????????? N) ????? ?????????? 2 ? 3. ????? ?? 3 ???? ? N, ? ?? N ? 4, ? ????? ????? 3 ? 4 ?????????.
? ???????????????? ?????? ????????? ?????????? ? ???????? ????? ?? ?????? ????? ????? ?????????? ?????????????.

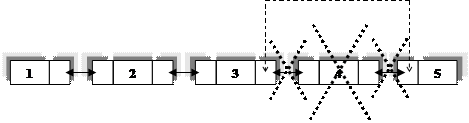Очередь (queue) — линейный список, в котором все включения производятся на одном конце списка, а все исключения (и обычно всякий доступ) делаются на другом его конце.

Очередь — тип данных, при котором новые данные располагаются следом за существующими в порядке поступления; поступившие первыми данные при этом обрабатываются первыми.

? ????????? ???????? ?????????? ????? "???????" ?????????? ? ????? ??????? ??????, ????????? ????? ???? ??????, ? ??????? ???????????? ????????? ? ??????????; ????????? ???? ??????????? ?????? ?????????? ????? "????????? ? ?????????? ????????????". ?????? ????? ?????? "???????" ???????????? ???? ? ????? ??????, ??????????? ????????????? ???????? ?????, ????????? ????????????.

Правило здесь такое же, как в живой очереди: первым пришёл—первым обслужен. Пришел новый покупатель, встал (добавился) в конец очереди, а который уже отоварился ушел (удалился) из начала очереди. То есть первым пришел, первым ушел.

Другими словами, у очереди есть голова (head) и хвост (tail). Элемент, добавляемый в очередь, оказывается в её хвосте, как только что подошедший покупатель; элемент, удаляемый из очереди, находится в её голове, как тот покупатель, что отстоял дольше всех.

? ??????? ????? ??????? ??????????? ?????? ? ?????? ?????. ???????? ???????? ?????????? ?? ?????? ?????. ? ?????? ?????? ??? ????? ???? ?????? 4 ???????. ??????? ?? ???? ???????????????? ??????, ?????? ?????????? ? ?????????? ????????? ?????????? ?? ?????? ??????.

Стек (stack) — линейный список, в котором все включения и исключения (и обычно всякий доступ) делаются в одном конце списка.

Стек — часть памяти ОЗУ компьютера, которая предназначается для временного хранения байтов, используемых микропроцессором; при этом используется порядок запоминания байтов «последним вошел – первым вышел», поскольку такие ввод и вывод организовывать проще всего, также операции осуществляются очень быстро. Действия со стеком производится при помощи регистра указателя стека. Любое повреждение этой части памяти приводит к фатальному сбою.

Стек в виде списка (pushdown list) – стек, организованный таким образом, что последний вводимый в область памяти элемент размещается на вершине списка.

Из стека мы всегда исключаем "младший" элемент из имеющихся в списке, т. е. тот, который был включен позже других. Для очереди справедливо в точности противоположное правило: исключается всегда самый "старший" элемент; узлы покидают список в том порядке, в котором они в него вошли.

Стеки очень часто встречаются в практике. Простым примером может служить ситуация, когда мы просматриваем множество данных и составляем список особых состояний или объектов, которые должны обрабатываться позднее; когда первоначальное множество обработано, мы возвращаемся к этому списку и выполняем последующую обработку, удаляя элементы из списка, пока список не станет пустым. Для этой цели пригодны как стек, так и очередь, но стек, как правило, удобнее. При решении задач наш мозг ведет себя как "стек": одна проблема приводит к другой, а та в свою оче­редь к следующей; мы накапливаем в стеке эти задачи и подзадачи и удаляем их по мере того, как они ре шаются. Аналогично процесс входов в подпрограммы и выходов из них при выполнении машинной программы подобен процессу функционирования стека. Стеки особенно полезны при обработке языков, имеющих структуру вложений. К ним относятся языки программирования, арифметические выражения и немецкие "Schachtelsatze" /буквально "вложенные предложения"/ . Вообще, стеки чаще всего возникают в связи с алгоритмами, имеющими явно или неяв­но рекурсивный характер.

Представьте себе, что четыре железнодорожных вагона находятся на входной стороне пути (рис. 1) и перенумерованы соответственно 1, 2, 3 и 4. Предположим, что мы выполняем следующую последовательность операций (которые согласуются с направлением стрелок на рисунке и не требуют, чтобы вагоны "перепрыгивали" друг через друга). Отправьте:

(а) вагон 1 в стек; « 1 2 3 4 5 6 » К-во Просмотров: 559 Бесплатно скачать Реферат: Линейные списки. Стек. Дек. Очередь >>> Скачать <<< Меню Поиск