Реферат: Математические игры и головоломки
Ниже приведён список самых распространённых “минимальных” операций, которыми пользуются при собирании кубика Рубика. Следует заметить, что это лишь универсальные комбинации, а для создания более совершенного алгоритма собирания кубика, нужно разработать более “глобальные” операции, которые человеку запомнить довольно трудно, но в общем уменьшающие количество действий, необходимых для собирания кубика из каждого конкретного положения.
Первый слой
|
Н ’П ’НП
|
НЛН ’Л ’
|
Сложная лесенка:
Н’П’Н2 П
Второй слой
|
НЛН’Л’Н’Ф’НФ
|
Н’П’НПНФН’Ф’
Третий слой
|
Выполняются только по две комбинации с поворотом верхней грани между ними:
(ПСн)4
|
Операция “Обмен” 1:
Ф2 В ’СпВ 2 СлВ ’Ф 2
 Операция “Обмен” 2:
Операция “Обмен” 2:
Л’Т’П’ТЛТ’ПТ
|
(Ф ’ПФП ’)2
|
(ПФ ’П ’Ф) 2
“Игры с дыркой”
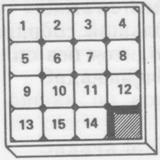
До изобретения кубика Рубика для многих людей знакомство с головоломками начиналось с “пятнашек” – так часто называют известную игру “15”.
С пятнашек начинается история игр с дыркой – головоломок, в которых фишки перемещаются по игровому полю за счёт того, что одно из мест на поле свободно. У “пятнашек” есть множество родственников, которые как раз и образовывают целый раздел этих головоломок.
Игру “15” придумал в 70-х годах XIX-го века прославленный американский изобретатель головоломок Сэмюэль Лойд. Время появления его игрушки и известного всем кубика Рубика разделяют ровно сто лет. Любопытно, что возраст обоих изобретателей, когда они придумали свои знаменитые головоломки, был одинаков – немногим больше тридцати. До “пятнашек” никакая другая головоломка таким успехом не пользовалась.
Великий Марк Твен, будучи современником Лойда и свидетелем всеобщего ажиотажа вокруг игры “15”, включил в свою сатирическую повесть “Американский претендент” изложение сообщения, якобы переданного агентством “Ассошиэйтед пресс”, в котором говорилось, что “за последние несколько недель вошла в моду новая игрушка-головоломка... и что от Атлантического океана до Тихого все население Соединенных Штатов прекратило работу и занимается только этой игрушкой; что в связи с этим вся деловая жизнь в стране замерла, ибо судьи, адвокаты, взломщики, священники, воры, торговцы, рабочие, убийцы, женщины, дети, грудные младенцы,— словом, все с утра до ночи заняты одним-единственным высокоинтеллектуальным и сложным делом... что веселье и радость покинули народ,— на смену им пришли озабоченность, задумчивость, тревога, лица у всех вытянулись, на них появились отчаяние и морщины — следы прожитых лет и пережитых трудностей, а вместе с ними и более печальные признаки, указывающие на умственную неполноценность и начинающееся помешательство; что в восьми городах день и ночь работают фабрики, и все же до сих пор не удалось удовлетворить спрос на головоломку”.
Вскоре после своего появления на свет коробочка с цифрами 15 на крышке пересекла океан, быстро распространилась во всех европейских странах и поучила новое имя “такен”. Изобретателю посчастливилось найти ту неуловимую меру сложности, когда головоломка решалась без труда почти всеми и в то же время требовала определённой сообразительности, благодаря чему каждый мог получить удовольствие от сознания своего высокого интеллектуального уровня.
|
Помещая это объявление, Лойд знал, что ничем не рискует, так как предлагает неразрешимую задачу. Эта задача ещё сыграла с изобретателем злую шутку, когда он пытался запатентовать свою игру, – ему сказали, что нельзя запатентовать игру, не имеющую решения.
Секрет игры “15”
Не всегда можно головоломку перевести из одного состояния в другое, — запрещены такие переходы, при которых нарушаются те или другие законы сохранения. Есть такой закон и в игре “15”. Чтобы объяснить его, мысленно заполним пустое место фишкой с номером 16. Тогда каждый ход — сдвиг фишки — будет состоять в том, что эта фишка меняется местами с фишкой 16. Операцию, при которой какие-то две фишки (не обязательно соседние!) меняются местами, так и назовем — обменом; математический термин для таких операций — транспозиция. Очевидно, что из любой расстановки 16 фишек можно не более чем за 15 обменов получитьправильную позицию — обозначим ее S0 — и вообще любую другую расстановку. При этих обменах не запрещается вынимать фишки из коробки. Например, можно сначала поставить на свое место фишку 1, обменяв ее с той фишкой, которая это место занимает, затем точно так же поставить на место фишку 2 и т. д. Последними мы обменяем фишки 15 и 16 — при этом сразу обе встанут правильно. Конечно, не исключено, что по ходу дела какие-то фишки автоматически попадут на свои места, и их трогать не придется, при этом число обменов окажется меньше 15. Можно расставлять фишки по этой же системе, но в другом порядке, скажем 16, 15, 14, .... или совсем иначе, и тогда число обменов может оказаться другим. Однако, каким бы способом ни выбрать последовательность обменов, превращающую одну заданную расстановку фишек в другую, четность числа обменов в этой последовательности всегда будет одной и той же.
Это очень важное и неочевидное докажем ниже. Оно позволяет дать следующее определение: расстановка называется четной, если ее можно превратить в правильную позицию с помощью четного числа обменов, и нечетной в противном случае. В математике обычно говорят не “расстановка”, а “перестановка”; к этому мы еще вернемся. Сама правильная расстановка S0 всегда четная , а ловушка Лойда L нечетная . Но почему они не переводятся друг в друга?
Как выше уже сказано, каждый ход в игре “15” можно рассматривать как обмен фишки с одной из соседних. Следовательно, при каждом ходе четность расстановки 16 фишек меняется: если до хода расстановку можно было упорядочить за N обменов, то после него — за N+1 обменов (взяв этот ход назад), а числа N и N+1 — разной четности. В обеих расстановках классической задачи Лойда дырка (или фишка 16) расположена одинаково. Если бы мы сумели одну расстановку перевести в другую, то фишка 16 должна была совершить столько же ходов вверх, сколько вниз, и столько же ходов вправо, сколько влево, иначе она не вернулась бы назад. Поэтому мы сделали бы четное число ходов, а так как при каждом ходе четность расстановки меняется, в начале и в конце она была бы одинаковой. Но позиции S0 и L, как мы видели, имеют разную четность.