Реферат: Метод половинного деления

Впрочем, это нетрудно найти. Выразим время полета снаряда на расстояние S из первой формулы:

,

и подставим во вторую:

Следуя нашей задаче, нам требуется найти такое значение угла наклона α, чтобы снаряд, пролетев заданное расстояние S , попал на нужную высоту Н .

Математик тут бы сказал, что надо решить уравнение. Мы тоже будем решать, только приближенно и очень похоже на то, как делают настоящие артиллеристы. Они же поступают следующим образом: производят несколько выстрелов, беря цель «в вилку», т.е. одно попадание выше цели, а другое ниже. Затем делят пополам угол между этими выстрелами, и при стрельбе под таким углом снаряд ложится к цели намного ближе. Но если все же не попали, то новую «вилку» снова делят пополам и т.д.

Мы заранее можем указать «вилку» для угла: 0 и π/4 (мы надеемся, что вы помните какой угол имеет радианную меру π/4 и чему приближенно равно π ). А дальше будем делить пополам эту «вилку» и смотреть, куда попадает снаряд, пока не добьемся нужного результата.

Как же долго нам придется вести «пристрелку», чтобы получить угол α , с нужной точностью? Чтобы ответить на этот вопрос, отвлечемся от нашей задачи и сформулируем на чисто математическом языке, что и как мы находили.

Нам даны некоторая функция f(x) и отрезок [a;b] , причем на концах этого отрезка эта функция принимает значения противоположных знаков. Если функция непрерывна, т.е. ее график – непрерывная линия, то ясно, что график функции пересекает ось абцисс в некоторой точке с отрезка [a;b] , как показано на рисунке 1. Иными словами, f(c) =0 , т.е. с - корень уравнения f(x)=0 .

Как же предлагается находить этот корень? А вот так. Делим отрезок [a;b] пополам, т.е. берем середину отрезка а+ b/2 . В этой точке вычисляем значение функции f(x) (рис. 2). Если это значение 0, то корень найден; если нет, то оно имеет тот же знак, что и значение на одном из концов отрезка [a;b] . Тогда этот конец заменям точкой а+ b/2 . Новый отрезок тоже содержит корень уравнения f(x)=0 , поскольку на его концах функция f(x) снова имеет разные знаки. Однако этот отрезок в 2 раза короче предыдущего. И самое главное – с ним можно поступить точно так же . со следующим отрезком еще раз проделать то же самое и т.д. поскольку длина отрезка каждый раз уменьшается вдвое, мы можем получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x)=0 . Например, если исходный отрезок был [3;4] , т.е. имел длину 1 , то через десять шагов мы получим отрезок длиной . Это означает, что концы отрезка дают нам приближенное значение корня с точностью, равной длине отрезка: левый конец отрезка – приближенное значение корня с недостатком, правый конец – приближенное значение корня с избытком.

Фактически мы сейчас сформулировали метод приближенного решения уравнения f(x)=0 . Его можно было бы назвать методом артиллерийской пристрелки. Но математики называют его методом половинного деления .

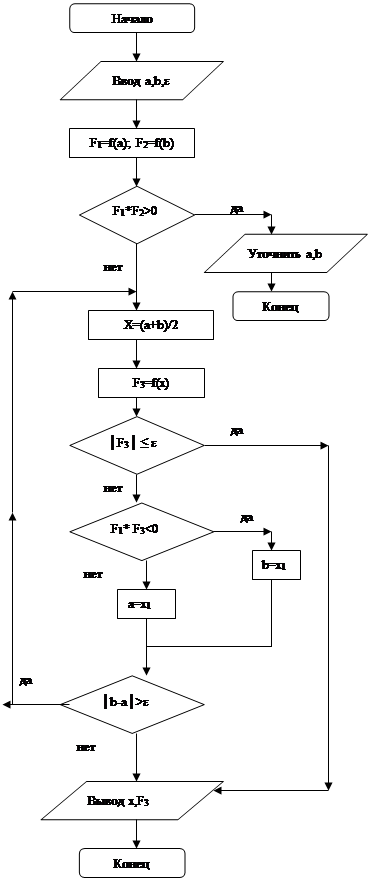
Далее ученикам предлагается записать алгоритм и блок-схему нахождения корня уравнения с помощью метода половинного деления.

Алгоритм

1) Найдем середину отрезка [ a; b ] : c = (a+b) /2 ;

2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d =f( c )ּf( a ) ;

3) Если d >0 , то теперь точкой a станет c : a = c ; Если d <0 , то точкой b станет c : b = c ;

4) Вычислим разность a и b , сравним ее с точностью ε : если |a-b |> ε , то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=( a+b )/2 ;

Блок - схема

Заключение

Информатике трудно существовать в школе как отдельной науке, она должна помогать другим учебным предметам в развитии познавательного интереса к предмету, в решении логических задач, в обработке результатов лабораторных работ и индивидуальных практических заданий. Школьники начинают испытывать удовлетворение, замечая, что элементы математики и информатики имеют реальное воплощение в физических процессах.

Математика является необходимой базой, которая позволяет глубже вникнуть в суть описываемых физических явлений и закономерностей. Hа уроках физики развиваются и конкретизируются многие математические понятия: функции, графики, уравнения, неравенство, производная, интеграл, вектор и др. Это требует согласованных действий от учителя физики и математики при формировании общих понятий.

В применении информатики к преподаванию других предметов используются в основном две формы работы: привлечение программных средств для контроля знаний учащихся и работа учащихся с обучающими программами. В стороне остаются возможности составления программ самими учащимися для решения тех или иных задач, например, из области физики. Среди методистов распространено мнение, что подобная работа в школе возможна лишь на высоком уровне (в специализированных классах) из-за слабой подготовки учащихся в области программирования. Однако при согласованных действиях преподавателей физики, математики и информатики этот недостаток может быть легко выполнен. В частности успешным оказывается проведение уроков по теме "Движение тела под действием силы тяжести при начальной скорости управления горизонтально или под углом к горизонту", изучаемой в курсе физики 9 класса совместно с учителем информатики. В курсе информатики Учащимся предлагается лабораторная работа "Артиллериская задача". При выполнении данной работы учитель отрабатывает навыки программирования, изучает метод дихотомии (половинного деления). При этом приходится решать задачу физически, т.е. возникают трудности по применению формул физики. Таким образом затмевается главная цель урока по информатике: формирование умений и навыков решения задач методом половинного деления с использованием ЭВМ. Поэтому здесь и необходимо проведение интегрированных уроков по физике и информатике при решении задач. Тем более, что в Сборник задач по физике для 9-11 классов (переизданного в 1992 г.), автором которого является А.П. Рымкевич, включены программируемые задачи, которые для решения требуют знаний по физике и информатике.

Литература

1. Гейн А.Г., А.И. Сенокосов, Н.А. Юнерман «Информатика: учебное пособие для 10-11 классов». М.: Просвещение, 2001.

2. Гейн А.Г., В.Г. Житомирский, Е.В. Линецкий, М.В. Сапир, В.Ф. Шолохович «Основы информатики и вычислительной техники». М.: Просвещение, 1992.

3. Симонович С., Г. Евсеев. «Практическая информатика: Учебное пособие для средней школы. Универсальный курс». – М.: Аст-пресс: Инфорком-пресс, 2001.

4. Сеть Internet

Приложение

Тематическое планирование уроков в 11 классе (68 часов).

№	Тема урока	Краткое содержание
1	Циклическая форма организации действий.	Циклы "до" и "пока". Вложенные и последовательные циклы.
2	Использование циклических структур при вычислении суммы произведения или количества множества произвольных числовых констант.	Рассмотрение таблицы предписаний для вычисления суммы произведения и количества множества чисел.
3	Циклическая структура как частный случай разветвляющегося алгоритма.	Решение задач, представляющих циклическую структуру с помощью операторов IF… THEN… GOTO. Операторы WHILЕ и WEND.
4	Цикл с параметрами.	Цикл для каждого и его параметры. Операторы FOR… TO… NEXT в цикле с параметрами.
5	Вводный инструктаж по ТБ.	« 1 2 3 4 5 6 » К-во Просмотров: 538 Бесплатно скачать Реферат: Метод половинного деления >>> Скачать <<< Меню Поиск