Реферат: Модели Атомного Ядра

Эта сравнительно небольшая поправка оказывается, однако, весьма существенной для ряда явлений и, в частности, для процесса деления тяжёлых ядер. Именно она определяет делимость ядер нечётных по А изотопов урана под действием медленных нейтронов, что и обусловливает выделенную роль этих изотопов в ядерной энергетике. Все константы, входящие в формулу (5), подбираются так, чтобы наилучшим образом удовлетворить эмпирическим данным. Оптимальное согласие с опытом достигается при e = 14,03 Мэв, a = 13,03 Мэв, b = 0,5835 Мэв, g= 77,25 Мэв. Формулы (5) и (6) могут быть использованы для оценки энергий связи ядер, не слишком удалённых от полосы стабильности ядер. Последняя определяется положением максимума x_св как функции Z при фиксированном А. Это условие определяет связь между Z и А для стабильных ядер:

Z=A (1,98+0,15A^2/3 )^-1 (7)

Формулы типа (5) не учитывают квантовых эффектов, связанных с деталями структуры ядер, которые могут приводить к скачкообразным изменениям x_св вблизи некоторых значений А и Z (см. ниже).

Структурные особенности в зависимости x_св от A и Z могут сказаться весьма существенно в вопросе о предельном возможном значении Z, т. е. о границе периодической системы элементов. Эта граница обусловлена неустойчивостью тяжёлых ядер относительно процесса деления. Теоретические оценки вероятности спонтанного деления ядер не исключают возможности существования «островов стабильности» сверхтяжёлых ядер вблизи Z = 114 и Z = 126.

Квантовые характеристики ядер.

Я. а. может находиться в разных квантовых состояниях, отличающихся друг от друга значением энергии и других сохраняющихся во времени физических величин. Состояние с наименьшей возможной для данного ядра энергией называется основным, все остальные — возбуждёнными. К числу важнейших квантовых характеристик ядерного состояния относятся спин I и чётность Р. Спин I — целое число у ядер с чётным А и полуцелое при нечётном. Чётность состояния Р = ± 1 указывает на изменение знака волновой функции ядра при зеркальном отображении пространства. Эти две характеристики часто объединяют единым символом I^P или I^± . Имеет место следующее эмпирическое правило: для основных состояний ядер с чётными А и Z спин равен 0, а волновая функция чётная (I^P = 0⁺ ). Квантовое состояние системы имеет определённую чётность Р, если система зеркально симметрична (т. е. переходит сама в себя при зеркальном отражении). В ядрах зеркальная симметрия несколько нарушена из-за наличия слабого взаимодействия между нуклонами, не сохраняющего чётность (его интенсивность по порядку величины ~ 10^-5 % от основных сил, связывающих нуклоны в ядрах). Однако обусловленное слабым взаимодействием смешивание состояний с разной чётностью мало и практически не сказывается на структуре ядер.

Помимо I и Р, ядерные состояния характеризуются также квантовыми числами, возникающими вследствие динамической симметрии ядерных взаимодействий. Важнейшей из них является изотопическая инвариантность ядерных сил. Она приводит к появлению у лёгких ядер (Z £ 20) квантового числа, называется изотопическим спином, или изоспином. Изоспин ядра T — целое число при чётном A и полуцелое — при нечётном. Различные состояния ядра могут иметь разный изоспин: T ³ (А— 2Z)/2. Известно эмпирическое правило, согласно которому изоспины основных состояний ядер минимальны, т. е. равны (А — 2Z)/2. Изоспин характеризует свойства симметрии волновой функции данного состояния ядра относительно замены p Û n. С изоспином связано существование изотопических ядерных мультиплетов или аналоговых состояний у ядер с одним и тем же А. Эти состояния, хотя и принадлежат разным ядрам (отличающимся по Z и N), имеют одинаковую структуру и, следовательно, одинаковые I^P и Т. Число таких состояний равно 2T + 1. Легчайшее после протона ядро — дейтрон имеет изоспин Т = 0 и поэтому не имеет аналогов. Ядра ³ ₁ H и ³ ₂ He образуют изотопический дублет с T = ¹ /₂ . В случае более тяжёлых ядер членами одного изотопического мультиплета являются как основные, так и возбуждённые состояния ядер. Это связано с тем, что при изменении Z меняется кулоновская энергия ядра (она растет с числом протонов), и, кроме того, при замене р Û n на полной энергии ядра сказывается разность масс протона и нейтрона. Примером изотопического мультиплета, содержащим как основные, так и возбуждённые состояния, является триплет с Т= 1: ¹⁴ ₈ C (осн) — ¹⁴ ₇ N (2,31 Мэв) ® ¹⁴ ₈ O (осн) (в скобках указана энергия возбуждения). Полуразность числа нейтронов и протонов, называется проекцией изоспина, обозначается символом Т_з . Для членов изотопического мультиплета Т_з принимает T + 1 значений, отличающихся друг от друга на единицу и лежащих в интервале —Т£ Т_з £ T. Величина Т_з для ядер определена так, что для протона Т_з = —¹ /₂ , а для нейтрона Т_з = + ¹ /₂ . В физике же элементарных частиц протону приписывается положительное значение Т_з , а нейтрону — отрицательное. Это чисто условное различие в определениях вызвано соображениями удобства (при избранном в ядерной физике определении Т_з эта величина положительна для большинства ядер).

«Чистота» состояний лёгких ядер по изоспину велика — примеси по порядку величины не превосходят 0,1—1%. Для тяжёлых ядер изоспин не является хорошим квантовым числом (состояния с разным изоспином смешиваются главным образом из-за электростатического взаимодействия протонов). Тем не менее, ощутимые следы изотопической симметрии остаются и в этом случае. Она проявляется, в частности, в наличии так называемых аналоговых резонансов (аналоговых состояний, не стабильных относительно распада с испусканием нуклонов).

Кроме I, P и T, ядерные состояния могут характеризоваться также квантовыми числами, связанными с конкретной моделью, привлекаемой для приближённого описания ядра (см. ниже).

Электрические и магнитные моменты ядер.

В различных состояниях ядро может иметь разные по величине магнитные дипольные и квадрупольные электрические моменты. Последние могут быть отличны от нуля только в том случае, когда спин I > ¹ /₂ . Ядерное состояние с определённой чётностью P не может обладать электрическим дипольным моментом. Более того, даже при несохранении чётности для возникновения электрического дипольного момента необходимо, чтобы взаимодействие нуклонов было необратимо во времени (T — неинвариантно). Поскольку по экспериментальным данным Т-неинвариантные межнуклонные силы (если они вообще есть) по меньшей мере в 10³ раз слабее основных ядерных сил, а эффекты несохранения чётности также очень малы, то электрические дипольные моменты либо равны нулю, либо столь малы, что их обнаружение находится вне пределов возможности современного ядерного эксперимента. Ядерные магнитные дипольные моменты имеют порядок величины ядерного магнетона. Электрические квадрупольные моменты изменяются в очень широких пределах: от величин порядка е·10^-27 см² (лёгкие ядра) до е·10^-23 см² (тяжёлые ядра, е — заряд электрона). В большинстве случаев известны лишь магнитные и электрические моменты основных состояний, поскольку они могут быть измерены оптическими и радиоспектроскопическими методами (см. Ядерный магнитный резонанс). Значения моментов существенно зависят от структуры ядра, распределения в нём заряда и токов. Объяснение наблюдаемых величин магнитных дипольных и электрических квадрупольных моментов является пробным камнем для любой модели ядра.

Структура ядра и модели ядер.

Многочастичная квантовая система с сильным взаимодействием, каковой является Я. а., с теоретической точки зрения объект исключительно сложный. Трудности связаны не только с количественно точными вычислениями физических величин, характеризующих ядро, но даже с качественным пониманием основных свойств ядерных состояний, спектра энергетических уровней, механизма ядерных реакций. Тяжёлые ядра содержат много нуклонов, но всё же их число не столь велико, чтобы можно было с уверенностью воспользоваться методами статистической физики, как это делается в теории конденсированных сред. К математическим трудностям теории добавляется недостаточная определённость исходных данных о ядерных силах. Поскольку межнуклонное взаимодействие сводится к обмену мезонами, объяснение свойств ядра в конечном счёте должно опираться на релятивистскую квантовую теорию элементарных частиц, которая сама по себе в современном её состоянии не свободна от внутренних противоречий и не может считаться завершенной. Хотя сравнительно небольшие в среднем скорости нуклонов в ядре (0,1 с) несколько упрощают теорию, позволяя строить её в первом приближении на основе нерелятивистской квантовой механики, ядерная задача многих тел остаётся пока одной из фундаментальных проблем физики. По всем этим причинам до сих пор, исходя из «первых принципов», рассматривалась только структура простейших ядер — дейтрона и трёхнуклонных ядер ³ H и ³ He. Структуру более сложных ядер пытаются понять с помощью ядерных моделей, в которых ядро гипотетически уподобляется какой-либо более простой и лучше изученной физической системе.

Оболочечная модель.

Её прообразом является многоэлектронный атом. Согласно этой модели, каждый нуклон находится в ядре в определённом индивидуальном квантовом состоянии, характеризуемом энергией, моментом вращения j его проекцией m на одну из координатных осей и орбитальным моментом вращения l = j± ¹ /₂ [чётность состояния нуклона P = (—1) ^l ]. Энергия уровня не зависит от проекции момента вращения на внешнюю ось. Поэтому в соответствии с Паули принципом на каждом энергетическом уровне с моментами j, l может находиться (2j + 1) тождественных нуклонов (протонов и нейтронов), образующих «оболочку» (j, l). Полный момент вращения заполненной оболочки равен нулю. Поэтому если ядро составлено только из заполненных протонных и нейтронных оболочек, то его спин будет также равен нулю. Всякий раз, когда количество протонов или нейтронов достигает магического числа, отвечающего заполнению очередной оболочки, возникает возможность скачкообразного изменения некоторых характеризующих ядро величин (в частности, энергии связи). Это создаёт подобие периодичности в свойствах ядер в зависимости от A и Z, аналогичной периодическому закону для атомов. В обоих случаях физической причиной периодичности является принцип Паули, запрещающий двум тождественным фермионам (частицам с полуцелыми спинами) находиться в одном и том же состоянии. Однако оболочечная структура у ядер проявляется значительно слабее, чем в атомах. Происходит это главным образом потому, что в ядрах индивидуальные квантовые состояния частиц («орбиты») возмущаются взаимодействием («столкновениями») их друг с другом гораздо сильнее, чем в атомах. Более того, известно, что большое число ядерных состояний совсем не похоже на совокупность движущихся в ядре независимо друг от друга нуклонов, т. е. не может быть объяснено в рамках оболочечной модели. Наличие таких коллективных состояний указывает на то, что представления об индивидуальных нуклонных орбитах являются скорее методическим базисом теории, удобным для описания некоторых состояний ядра, чем физической реальностью.

В этой связи в оболочечную модель вводится понятие квазичастиц — элементарных возбуждений среды, эффективно ведущих себя во многих отношениях подобно частицам. При этом Я. а. рассматривается как квантовая жидкость, точнее как ферми-жидкость конечных размеров. Ядро в основном состоянии рассматривается как вырожденный ферми-газ квазичастиц, которые эффективно не взаимодействуют друг с другом, поскольку всякий акт столкновения, изменяющий индивидуальные состояния квазичастиц, запрещен принципом Паули. В возбуждённом состоянии ядра, когда 1 или 2 квазичастицы находятся на более высоких индивидуальных энергетических уровнях, эти частицы, освободив орбиты, занимавшиеся ими ранее внутри ферми-сферы, могут взаимодействовать как друг с другом, так и с образовавшейся дыркой в нижней оболочке. В результате взаимодействия с внешней квазичастицей может происходить переход квазичастиц из заполненных состояний в незаполненное, вследствие чего старая дырка исчезает, а новая появляется; это эквивалентно переходу дырки из одного состояния в другое. Т. о., согласно оболочечной модели, основывающейся на теории квантовой ферми-жидкости, спектр нижних возбуждённых состояний ядер определяется движением 1—2 квазичастиц вне ферми-сферы и взаимодействием их друг с другом и с дырками внутри ферми-сферы. Этим самым объяснение структуры многонуклонного ядра при небольшых энергиях возбуждения фактически сводится к квантовой проблеме 2—4 взаимодействующих тел (квазичастица — дырка или 2 квазичастицы — 2 дырки). Применение теории ферми-жидкости к Я. а. было развито А. Б. Мигдалом (1965). Трудность теории состоит, однако, в том, что взаимодействие квазичастиц и дырок не мало и потому нет уверенности в невозможности появления низкоэнергетического возбуждённого состояния, обусловленного большим числом квазичастиц вне ферми-сферы.

В других вариантах оболочечной модели вводится эффективное взаимодействие между квазичастицами в каждой оболочке, приводящее к перемешиванию первоначальных конфигураций индивидуальных состояний. Это взаимодействие учитывается по методике теории возмущений (справедливой для малых возмущений). Внутренняя непоследовательность такой схемы состоит в том, что эффективное взаимодействие, необходимое теории для описания опытных фактов, оказывается отнюдь не слабым. Кроме того, как показывает сравнение теоретических и экспериментальных данных, в разных оболочках приходится вводить разные эффективные взаимодействия, что увеличивает число эмпирически подбираемых параметров модели.

Основные теоретические разновидности модели оболочек модифицируются иногда введением различного рода дополнит, взаимодействий (например, взаимодействия квазичастиц с колебаниями поверхности ядра) для достижения лучшего согласия теории с экспериментом.

Т. о., современная оболочечная модель ядра фактически является полуэмпирической схемой, позволяющей понять некоторые закономерности в структуре ядер, но не способной последовательно количественно описать свойства ядра. В частности, ввиду перечисленных трудностей непросто выяснить теоретически порядок заполнения оболочек, а следовательно, и «магические числа», которые служили бы аналогами периодов таблицы Менделеева для атомов. Порядок заполнения оболочек зависит, во-первых, от характера силового поля, которое определяет индивидуальные состояния квазичастиц, и, во-вторых, от смешивания конфигураций. Последнее обычно принимается во внимание лишь для незаполненных оболочек. Наблюдаемые на опыте магические числа нейтронов (2, 8, 20, 28, 40, 50, 82, 126) и протонов (2, 8, 20, 28, 50, 82) отвечают квантовым состояниям квазичастиц, движущихся в прямоугольной или осцилляторной потенциальной яме со спин-орбитальным взаимодействием (именно благодаря ему возникают числа 28, 40, 82 и 126). Объяснение самого факта существования магических чисел было крупным успехом модели оболочек, впервые предложенной М. Гёпперт-Майер и Й. Х. Д. Йенсеном в 1949—50.

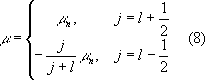??. ?????? ??????????? ?????? ???????? ???? ? ?????????? ????? (??? ????? ?????????????? ???????????) ???????? ????????? ????????? ????? ???????? ????????? ???????? ???? ? ???????????? ???????? ?????? ? ????????? ????????? ???????? ????? ????. ???????? ??????????? ??????, ??? ???????? ??? ???????? ???? ???????????? ?????????? (?????????? j, I) ?????????? ?????????????? ???????. ? ???? ?????? I = j, P = (?1) ^l . ????????? ????????? ?????? m (? ??????? ??????????), ???? ??????????? ???????? ???????? ???????, ?????:
? ?????? ???????????? ???????:

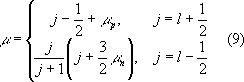Здесь m_n = 1,913 и m_p = 2,793 — магнитные моменты нейтрона и протона. Зависимости m от j при данном l = j ± ¹ /₂ называются линиями Шмидта. Магнитные дипольные моменты практически всех нечётных ядер, согласно опытным данным, лежат между линиями Шмидта, но не на самих линиях, как это требуется простейшей оболочечной моделью (рис. 1, 2). Тем не менее близость экспериментальных значений магнитных дипольных моментов ядер к линиям Шмидта такова, что, зная j — I и m, можно в большинстве случаев однозначно определить I. Данные о квадрупольных электрических моментах ядер значительно хуже описываются оболочечной моделью как по знаку, так и по абсолютной величине. Существенно, однако, что в зависимости квадрупольных моментов от А и Z наблюдается периодичность, соответствующая магическим числам.

Все эти сведения о ядрах (значения I^P , электрических и магнитных моментов основных состояний, магические числа, данные о возбуждённых состояниях) позволяют принять схему заполнения ядерных оболочек, приведённую на рис. 3.

Несферичность ядер. Ротационная модель.

???????? ????????????????? ?????? ? ??????? ???????? ????? 150 < A < 190 ? ? > 200, ????????????? ??????? Q ???? c I>¹ /₂ ??????????? ??????, ??? ?????????? ?? ????????, ??????????????? ??????????? ???????, ? 10?100 ???. ? ???? ?? ??????? ???????? ? ??????????? ??????? ?????? ???????????? ????????? ???? ?? ????? ???? ??????????? ???????????? ??????? ?? ??????????? ??????? ???????????? ?????? ?? ??? ??????? ????????. ???????? ????? ??? ???????? ? ???? ? ??????? ? ? Z. ? ???? ?????? ??????? x ????????????? ?????? ?? ?????? I ?????? ????????????:

(10)

??? J ? ????????, ??????????? ?? ????????? ?? I ? ??????? ??????????? ??????? ???????. ????? ???????????? ????????? ? (10) ?????????, ??? ?????????? ????, ?????? ?????? ????????: 2, 4, 6,... (????????????? ????????? ?????????). ??? ????? ????????? ?????????? ??? ??????????? ?????? ?????????????? ????, ???????????? ???????????? ??????? ??. ??????????? (1950) ? ???????? ? ??????? ???????? ?????? ?. ???? ? ????????????? ?????? ?. ??????????? ???????? ???? ??????, ???? ???????????? ????? ????????? ???????? ??? ??????? (a₁ ) ? ????? (a₂ ) ??????? ?????????? ????? ???????? ?????????? b ???? ?????????????:
(11)

Электрический квадрупольный момент Q несферического ядра выражается через b. Параметры b, определённые из данных по квадрупольным моментам (не только по статическим, но и динамическим — т. е. по вероятности испускания возбужденным ядром электрического квадрупольного излучения), оказываются по порядку величины равными 0,1, но варьируются в довольно широких пределах, достигая у некоторых ядер редкоземельных элементов значений, близких к 0,5. От параметра b зависит также момент инерции ядра. Как показывает сравнение опытных данных по энергии возбужденных состояний несферических ядер с формулой (10), наблюдаемые значения J значительно меньше моментов инерции твёрдого эллипсоида вращения относительно направления, перпендикулярного оси симметрии. Нет так же ротационных уровней, соответствующих вращению эллипсоида вокруг оси симметрии. Эти обстоятельства исключают возможность отождествить вращение несферического ядра с квантовым вращением твердотельного волчка в буквальном смысле слова. Для ротационной модели несферических ядер принимается схема, аналогичная квантованию движения двухатомной молекулы с идентичными бесспиновыми ядрами: вращательный момент ядер такой молекулы относительно её центра тяжести всегда перпендикулярен оси симметрии (линии, соединяющей ядра). Из-за свойств симметрии волновой функции относительно перестановки ядер допустимы только чётные значения момента вращения (0, 2, 4 и т. д.), что как раз соответствует значениям I для ротационных состояний несферических ядер с чётными А и Z. Для ядер с небольшими значениями параметров деформации b, наблюдаемые значения близки к моменту инерции той части эллипсоида вращения, которая находится вне вписанного в эллипсоид шара. Такой момент инерции мог бы иметь идеальный газ, помещенный в сосуд в форме эллипсоида вращения, или, что то же самое, частицы, движущиеся независимо друг от друга в несферической эллипсоидальной потенциальной яме. С ростом b момент инерции ядра в такой модели растет довольно быстро, достигая твердотельного значения. Это противоречит опытным данным, согласно которым рост l с увеличением Р происходит значительно медленнее, так что для реальных ядер I принимают значения, лежащие между моментами инерции части эллипсоида, находящейся вне вписанного в него шара и твёрдого эллипсоида вращения. Это противоречие устраняется учётом взаимодействия между частицами, движущимися в потенциальной яме. При этом, как оказывается, гл. роль играют парные корреляции «сверхтекучего типа» (см. ниже).

Описанная картина структуры несферического ядра отвечает обобщению оболочечной модели на случай движения квазичастиц в сферически-несимметричном потенциальном поле (обобщённая модель). При этом несколько изменяются и схема энергетических уровней и квантовые числа, характеризующие индивидуальные орбиты частиц. В связи с появлением физически выделенного направления — оси симметрии эллипсоида, сохраняется проекция момента вращения каждой из частиц на эту ось. Момент вращения частицы при этом перестаёт быть определённым квантовым числом. Практически, однако, для всех ядер смешивание орбит с разными j мало, так как несферичность ядра в движении частиц сказывается главным образом на появлении дополнительного квантового числа.

??? ???????? ???? ???? ???? I ?????????? ????????? ????????? ???????????? ??????? ????? ???? ??? ?????? ? ??????? ???????? ???????????? ????????? ???????. ??? ???? ??????? ???????????? ?????? ??????? ?? ?????? ?? I, ?? ? ?? ???????? ??????? ???????? ? ????????? ??????? ?? ??? ????????? ????. ?????? ????????? ? ???????? ?????? ???????????? ???????. ????? ???????, ???????????? ??????? x (I) ???????????? ?????? ????????? ????, ????? ???:

(12)

где d_K,1/2 = 0, если К ¹ ¹ /₂ и d_K,1/2 = 1. при K = ¹ /₂ ; a — эмпирически подбираемая константа, характеризующая «связь» момента вращения частицы и ротационного момента ядра. Моменты инерции для чётных и нечётных по А несферических ядер по порядку величины одинаковы и таковы, что энергия возбуждения первого ротационного уровня у ядер редкоземельных элементов около 100 кэв (это отвечает значениям J ~ 10^-47 г·см² ).

Существенная черта ротационной модели несферических ядер — сочетание вращения всего ядра, как целого, с движением отдельных нуклонов в несферическом потенциальном поле. При этом предполагается, что вращение всего ядра (т. е. несферической потенциальной ямы) происходит достаточно медленно сравнительно со скоростью движения нуклонов (адиабатическое приближение). Более точно последнее означает, что расстояние между соседними ротационными уровнями должно быть мало сравнительно с расстояниями между энергетическими уровнями нуклонов в потенциальной яме. Адиабатическое приближение для описания энергетического спектра некоторых несферических ядер оказывается недостаточным. В этом случае вводятся неадиабатические поправки (например, на кориолисовы силы и др.), что приводит к увеличению числа параметров, определяемых из сравнения теории с опытом.

Современные данные о ротационных спектрах несферических ядер обильны. У некоторых ядер известно несколько ротационных полос (например, у ядра ²³⁵ U наблюдается 9 полос, причём отдельные ротационные полосы «прослежены» вплоть до спинов I = ²⁵ /₂ и более). Несферические ядра в основном сосредоточены в области больших А. Есть попытки интерпретировать и некоторые лёгкие ядра как несферические (так в несферичности «подозревается» ядро ²⁴ Mg). Моменты инерции таких лёгких ядер оказываются примерно в 10 раз меньше, чем у тяжёлых.

Ротационная модель несферических ядер позволяет описать ряд существенных свойств большой группы ядер. Вместе с тем эта модель не является последовательной теорией, выведенной из «первых принципов». Её исходные положения постулированы в соответствии с эмпирическими данными о ядрах. В рамках этой модели необъяснённым остаётся сам факт возникновения ротационного спектра (т. е. факт вращения всего ядра, как целого). Попытки получить ядерные ротационные спектры на основе общей квантовомеханической теории системы многих тел пока остаются незавершёнными.

Сверхтекучесть ядерного вещества и другие ядерные модели.

Аналогично тому, как спаривание электронов в металлах порождает