Реферат: Натяжение жидкости. Принцип работы сталагмометра
![]() (3)
(3)
Площадь поверхности зависит от ее кривизны и дисперсности фаз (размера частиц или поверхностных дефектов). Дисперсность D линейно связана с удельной поверхностью Sуд:
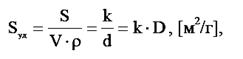 (4)
(4)
где: V - объем дисперсной фазы;
d - размер частиц;
k - коэффициент формы и плотности частицы.
Удельная поверхность, например, водяного тумана при радиусе капелек 1 мкм составит:
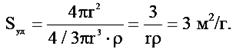 (5)
(5)
Стремление системы к уменьшению поверхностной энергии Гиббса выражается в самопроизвольном уменьшении межфазной поверхности (изменение формы и кривизны, проявление процессов коагуляции, коалесценции и пр.) и уменьшении поверхностного натяжения (протекание процессов адсорбции, адгезии и смачивания, возникновение электрического потенциала и др.)
Измерение коэффициента поверхностного натяжения по методу отрыва капель (сталагмометрия)
Метод отрыва капель, не будучи очень точным, является, однако распространенным в медицинской и фармацевтической практике. Теоретическое обоснование этого метода заключается в следующем. Образование капель жидкости при вытекании ее из малых отверстий является результатом действия силы поверхностного натяжения и силы тяжести. Так, если из вертикально поставленной трубки с узким капиллярным отверстием медленно вытекает жидкость, то на конце трубки образуется постепенно нарастающая по величине u1082 капля. Увеличиваясь в размере, эта капля отрывается тогда, когда ее вес становится равным сопротивлению разрыва поверхностной пленки, поддерживающей каплю.
Перед отрывом капли у конца трубки образуется перетяжка, по которой происходит отрыв капли (рис.3).

Рисунок 3 – Схема сталагмометра.
Сталагмометр представляет собой стеклянную трубку с расширением посередине и капилляром в нижней части; расширенная часть ограничена двумя метками. Поместив капилляр в стаканчик с исследуемым раствором, при помощи резиновой груши затягивают раствор в прибор (уровень жидкости должен быть выше верхней метки) и дают жидкости по каплям вытекать из сталагмометра в стаканчик. Скорость истечения можно регулировать при помощи винтового зажима. Когда уровень жидкости достигнет верхней метки, начинают отсчет капель; отсчет продолжают до достижения уровнем нижней метки.
Определение поверхностного натяжения этим методом заключается в измерении объема или веса капли жидкости, отрывающейся от кончика капилляра в нижнем конце сталагмометрической трубки.
В момент отрыва капли сила поверхностного натяжения fT уравновешивается силами поверхностного натяжения F. Сила поверхностного натяжения действует вдоль окружности шейки капли и препятствует ее отрыву. В момент отрыва можно считать, что длина контура, по которому разрывается поверхностная пленка капли, равна длине окружности перетяжки, и равна 2πr. Тогда сила поверхностного натяжения по всему контуру отрыва будет равна:
F=σ×l=2πrσ. (6)
Перед самым отрывом эта сила F уравновешивает силу тяжести mg. Силу тяжести чаще всего рассчитывают, определяя объем капли. Сталагмометрическую трубку определенного объема V заполняют исследуемой жидкостью и определяют число капель n, вытекающих из данного объема. Силу тяжести рассчитывают по уравнению:
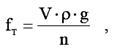 (7)
(7)
где р- плотность исследуемой жидкости.
В связи со сложностью измерения внутреннего диаметра капилляра (точнее - шейки капли) обычно поверхностное натяжение находят путем сравнения данных по истечению из сталагмометрической трубки исследуемой жидкости и жидкости с известным поверхностным натяжением (стандартной жидкости).
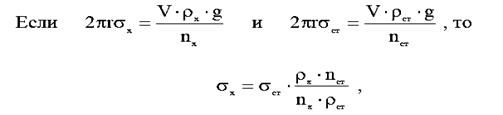 (8)
(8)
![]() - для искомой и стандартных жидкостей
- для искомой и стандартных жидкостей
Масса капли может быть легко определена, но определение радиуса перетяжки r связано с некоторыми затруднениями. Подставлять же в уравнение вместо радиуса перетяжки величину радиуса конца недопустимо, т.к. ее радиус всегда больше радиуса перетяжки. Метод, позволяющий избежать измерения радиуса перетяжки, заключается в сравнении коэффициента поверхностного натяжения σ1, исследуемой жидкости с коэффициентом поверхностного натяжения σ0 другой жидкости, для которой величина этого коэффициента хорошо известна. Обычно в качестве эталонной жидкости применяется вода, величина коэффициента которой для различных температур дается в таблицах. Тогда можно написать уравнения для исследуемой жидкости:
2πrσ1 = m1g . (9)
Для эталонной жидкости:
2πrσ0 = m0g . (10)
Здесь m1 и m0 – массы капель исследуемой и эталонной жидкостей и, а радиусы перетяжек капель обеих жидкостей приняты одинаковыми. Деля почленно выражение (9) на выражение (10), получим :