Реферат: Новые фундаментальные физические константы

где: m_э – электромагнитная масса, l – метрическая характеристика.

Из динамического закона следует, что электромагнитная масса принимает значения от некоторого минимального значения до некоторой предельной величины:

0 < m_э < m_max .

Это приводит к тому, что метрическая характеристика изменяется от некоторого максимального значения до некоторой предельной величины:

l_min < l < ∞ .

Уравнение (5) представляет собой динамический закон, который отображает динамическую симметрию вакуума. D-инвариантность вакуума является новым видом симметрии и отражает наиболее фундаментальное свойство Природы. С D-инвариантностью вакуума связан важнейший закон сохранения, который не нарушается при всех видах взаимодействий.

D-инвариантность вакуума является симметрией более высокого порядка, чем известные на сегодня симметрии. Нарушения симметрии, которые наблюдаются в Природе, вплоть до несохранения CP-инвариантности, не затрагивают D-инвариантность вакуума. Границей D-инвариантности являются фундаментальные константы m_e и l_u , что и отражает динамический закон вакуума. Таким образом, динамическая симетрия вакуума не противоречит идее развития, поскольку D-инвариантность сохраняется и тогда, когда нарушаются другие виды симметрии. В вакууме реализуется реальный физический процесс, обязанный своим существованием динамической симметрии, который приводит к появлению дискретных частиц из непрерывного физического объекта, что в математическом описании представлено как достижение физическими величинами своих предельных квантованных значений [5...14].

Из соотношений (2) и (4) следует, что:

R_u = c μ _v , (6)

где: μ _v – магнитная константа вакуума.

Из формулы для фундаментального кванта действия (2) следует новая формула для элементарного заряда e:

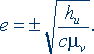(7)

В системе СГСЭ соотношение для элементарного заряда примет вид:

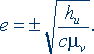(8)

Соотношения (7) и (8) представлены квадратным корнем. Из них непосредственно следует бинарность зарядов, т.е. то, что заряды имеют два знака. Поскольку заряды определяются только константами, то из этих соотношений следует также и квантованность зарядов.

Рассмотривая динамику невещественных объектов вакуума, легко видеть, что первым фиксированным значением энергии, которая соответствует устойчивому физическому объекту, является энергия электрона или позитрона E_e . Тогда значение частоты, которое соответствует этой величине энергии будет равно:

ν = E_e /h_u = 1,063870869·10²³ Гц.

Отсюда следует четвертая физическая константа вакуума – фундаментальный квант времени:

t_u = 0,939963701(11)·10^–23 с.

Используя константу скорости света c, получим пятую константу вакуума – фундаментальный квант длины:

l_u = 2,817940285(31)·10^–15 м.

Отметим, что значение этой константы в точности совпадает с классическим радиусом электрона. Все пять констант вакуума h_u , G_u , R_u , t_u , l_u получены на основе нового подхода к пониманию физической сущности полевых структур. Проведенные исследования этих констант показали, что используемые в современной физике фундаментальные физические константы непосредственно происходят от констант физического вакуума [6...8, 14]. Приведенные выше основные константы вакуума позволяют получить ряд вторичных констант, которые являются производными константами и также относятся к физическому вакууму.

Константы фундаментальной метрики t_u и l_u образуют новую константу b, названную фундаментальным ускорением [5]:

b = l_u /t_u ² .

Значение этой константы равно:

b = 3,189404629(36)·10³¹ м/с² .

Эта константа позволила получить новый закон силы [6, 8, 10, 15]

F = m·b.

Этот закон отражает связь силы с дефектом массы.