Реферат: Однозеркальная антенна

.

У длиннофокусного параболоида , у короткофокусного . При (фокус лежит в плоскости раскрыва зеркала) .

Апертурный метод расчет поля излучения.

В апертурном поле излучения зеркальной антенны находится по известному полю в ее раскрыве. В этом методе, в качестве излучающей рассматривается плоская поверхность раскрыва параболоида с синфазным полем и известным законом распределения его амплитуды.

Амплитудный метод в том виде, в котором он используется на практике, является менее точным, чем метод расчета через плотность тока. Это объясняется тем, что в этом случае поле в раскрыве зеркала находится по законам геометрической оптики. Следовательно, не учитывается векторный характер поля и, как результат этого, не учитывается составляющие с паразитной поляризацией. Однако в пределах главного лепестка и первых боковых лепестков, т.е. в наиболее важной для нас области диаграммы направленности, оба метода практически дают одинаковые результаты. Поэтому на практике наибольшее распространение получил апертурный метод расчета как более простой.

Задача нахождения поля излучения зеркальной антенны при апертурном методе расчета, как и в общей теории антенн разбивается на две:

1.Вначале находится поле в раскрыве антенны (внутренняя задача).

2.По известному полю в раскрыве определяется поле излучения (внешняя задача).

А). Определение поля в раскрыве параболоидного зеркала.

Поле в раскрыве определяется методом геометрической оптики. Всегда выполняется условие , следовательно, зеркало в дальней зоне и падающую от облучателя волну на участке от фокуса до поверхности зеркала можно считать сферической.

В сферической волне амплитуда поля изменяется обратно пропорционально . После отражения от поверхности зеркала волна становится плоской и амплитуда ее до раскрыва зеркала с расстоянием не изменяется. Таким образом, если нам известна нормированная диаграмма направленности облучателя , поле в раскрыве зеркала легко находится.

Для удобства расчетов введем нормированную координату точки в раскрыве зеркала

;

Подставим значение и

в выражение для , после элементарных преобразований получаем

.

Очевидно, что и меняется в пределах .

Нормированное значение амплитуды поля в раскрыве определится выражением .

Подставим в последнюю формулу значение , получим окончательно .

Полученная формула является расчетной. Из нее видно, что амплитуда поля в раскрыве зеркала зависит только от радиальной координаты . Такая осевая симметрия в распределении поля явилась следствием допущения, что диаграмма направленности облучателя является функцией только полярного угла и не зависит от азимутального угла , хотя эта зависимость обычно выражена слабо. Вследствие этого в большинстве случаев можно ограничиться расчетом распределения поля в раскрыве только вдоль двух главных взаимно перпендикулярных направлений: параллельного оси X и оси Y. Система координат X,Y,Z ориентируется так, чтобы эти направления лежали в плоскости вектора (плоскость XOZ) и вектора (плоскость YOZ). Для этих плоскостей затем и рассчитывается поле излучения и диаграмма направленности антенны. Расчет ведется в предположении, что поле в раскрыве зависит только от радиальной координаты , а диаграмма направленности облучателя при расчете в плоскости вектора есть , а при расчете в плоскости вектора есть .

Таким образом, распределение поля в плоскости вектора будет несколько отличаться от распределения в плоскости , что противоречит принятой зависимости распределения поля только от радиальной координаты. Однако вследствие небольшого различия между функциями и принятые допущения не приводят к существенным погрешностям в расчетах и в тоже время позволяют учесть различия в диаграмме направленности облучателя в плоскостях и .

И
з рис. видно, что наиболее интенсивно облучается центр зеркала, а поле к его краям по амплитуде падает вследствие уменьшения значения и увеличения с увеличением . Типичное распределение нормированной амплитуды поля в раскрыве параболоидного зеркала показано на рис.:

Для упрощения последующих расчетов найденное значение целесообразно аппроксимировать интерполяционным полиномом

.

Этот полином хорошо аппроксимирует фактическое распределение поля в раскрыве параболоида и для нахождения поля излучения при такой аппроксимации не потребуется громоздких вычислений. Излучение круглой площадки с распределением поля на ее поверхности, определяемым, уже было рассмотрено выше.

Узлами интерполяции, т.е. точками, где полином совпадает с ранее найденной функцией , будем считать точки раскрыва зеркала, соответствующие значениям : Тогда коэффициенты полинома определяется из системы уравнений:

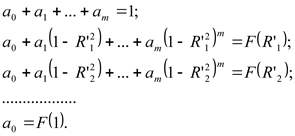
На этом решение задачи определения поля в раскрыве параболоида можно считать законченным.