Реферат: Определение точного коэффициента электропроводности из точного решения кинетического уравнения

Здесь при переходе от первой строки ко второй принято во внимание, что

òf⁰ _k ev_k (r)dk º 0,

использованы также формулы для преобразования объемного интеграла в k-пространстве в интеграл по изоэнергетическим поверхностям и по энергии.

В металле функция (– ¶f⁰ /¶E) ведет себя как d-функция от (E – z), поэтому остается только проинтегрировать по поверхности Ферми. Таким образом,

(55)

Сравним это выражение с обычной макроскопической формулой

J = s×E, (56)

где s – тензор. Получим

(57)

Обычно имеют дело с кристаллами кубической симметрии,при этом тензор электропроводности сводится к скаляру, помноженному на единичный тензор. В случае, когда оба вектора E и J направлены по оси х, подынтегральное выражение в (55) есть

(v_k v_k × E) = v² _x E, (58)

что дает 1/3 вклада от квадрата скорости, v² E. Поэтому

(59)

где мы ввели длину свободного пробега

L = tv. (60)

Это есть основная формула для электропроводности.

Интересно посмотреть (фиг. 97), как выглядит функция распределения f_k , заданная выражением (7.8). Как видно из равенства (53), функция g_k велика только вблизи поверхности Ферми.

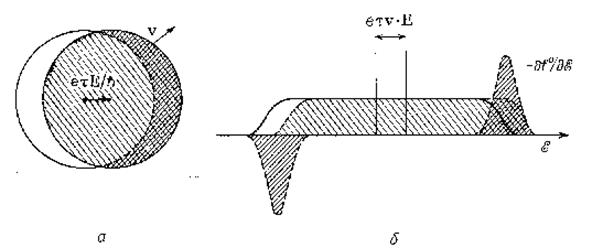
Фиг.97. а – смещенная поверхность Ферми; б – смещенное распределение Ферми.

Небольшая добавка появляется с той стороны, где v_k ×eE>0, т. е. там, где электроны ускоряются полем. Та же величина вычитается с противоположной стороны.

Фактически по теореме Тейлора можно написать

(61)

Это выглядит так, как будто вся сфера Ферми сдвинулась в k-пpoстранстве на величину (et/ħ)E. Это несколько неверная интерпретация. В действительности поле не действует на состояния вблизи дна зоны, в глубине сферы Ферми. Из-за принципа Паули поле не может придать ускорения электронам в таких состояниях; по этой же причине они не рассеиваются примесью.

Отметим, однако, что электропроводность не зависит от температуры (если не считать возможной температурной зависимости t). Эта же формула справедлива при T = 0, когда распределение Ферми имеет совершенно четкую границу. Можно сказать, что электропроводность выражается через смещение жесткой поверхности Ферми.

Заметим также, что выражение (61) можно представить в виде

f_k = f⁰ (E_k + etv_k E), (62)

как будто к энергии электрона в состоянии k добавилась величина

dE_k = etv_k E. (63)

Это в точности соответствует классической ситуации, которая имела бы место, если бы электрон со скоростью v_k двигался в поле E в течение интервала времени t. Это замечание лежит в основе кинетического метода решения подобных задач. Добавочная энергия, приобретаемая в промежутках между столкновениями с примесями, соответствует наличию дрейфовой скорости dv в направлении поля; именно

dv(¶E/¶v) = evEt, (64)

или для классической частицы массы m

dv(¶E/¶v) = evEt / mv. (65)

Пусть концентрация частиц есть n, тогда полная плотность тока равна

J = nedv, (66)

и, сравнивая формулы (65), (66) и (56), находим

s = ne² t/m. (7.33)

Легко показать, что в случае свободного электронного газа формулы (67) и (59) эквивалентны; в металле последняя формула принципиально значительно лучше. Она показывает, что электропроводность зависит только от свойств электронов на уровне Ферми, а не от полной концентрации их. Большую электропроводность металлов следует объяснять скорее наличием небольшой группы очень быстрых электронов на вершине распределения Ферми, а не высоким значением полной концентрации свободных электронов, которым можно придать небольшую дрейфовую скорость.

Основная формула (59) показывает также, что происходит, когда площадь свободной поверхности Ферми уменьшается в результате взаимодействия с границами зоны, и учитывает влияние решетки, ограничивающее эффективную скорость электронов на поверхности Ферми. Такие эффекты действительно можно наблюдать в металлах типа Bi.

С другой стороны, формула кинетической теории (67) удобна для полупроводников. При этом под п следует понимать концентрацию свободных носителей заряда. Обычно пишут

s = n|е|m (68)

где

m = |e|t/m (69)

есть подвижность носителей. В более общем случае считают, что электроны и дырки вносят независимые вклады в полный ток и определяют их подвижности равенством

s = n_h |е| m_h + n_e |е| m_e . (70)

Нетрудно вывести формулу (68), скажем, из (54), принимая в качестве f° классическую функцию распределения. При этом мы допускаем, что время релаксации t может зависеть от энергии; в формулу (69) надо подставить его среднее значение

(71)

где N(E) есть плотность состояний в рассматриваемой зоне. Таким образом,

m_e = |e|t_e /m_e (7.38)

где т_е — эффективная масса электронов. Аналогичная формула справедлива и для дырок. Из этих формул видно, что подвижность может зависеть от температуры. С ростом T распределение размазывается и среднее время релаксации изменяется. В случае металла то обстоятельство, что т зависит от энергии, не играет большой роли, ибо существенно только значение t (E_F ).