Реферат: Оптимизация отбора оптимальных признаков на основе приме-нения методов моделирования эволюции для задачи распозна-вания текста
Формула 3
Однако, субъективность группирования обуславливает неприемлемо длительный перебор при поиске оптимальных признаков. Отказываясь от заданности h(X), можно установить деление на группы в процессе поиска j(L,X). Такая возможность существует, так как j(L,X) и hp (X) однозначно связаны между собой, поскольку равенство |qp |=SN0 выполняется лишь тогда, когда знаки j(Lp ,X) и hp (X) либо одинаковы и qp =SN0 , либо противоположны и qp =(-SN0 ). Это позволяет при поиске j(Lp ,X) заменить критерий (Формула 3) эквивалентным
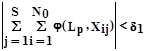
Формула 4
Введём двоичную переменную yp такую, что yp =0, если j(Lp ,X)=-1, и yp =1, если j(Lp ,X)=1. Совокупность m таких переменных может рассматриваться как искомое промежуточное изображение.
Недостатком критерия является то, что он может пропускать в число оптимальных признаки, сумма которых внутри образа близка к 0, то есть признаки, которые на половине изображений образа равны +1, а на другой половине изображений равны -1. В связи с малой информативностью таких признаков критерий целесообразно дополнить, расщепив его
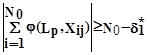
Формула 5
j=1,2,..,S.
где d* 1 - достаточно малая величина. Критерий определяет условие совпадения признака для большинства изображений каждого образа.
Тип признаков зависит от характера изображений конкретной задачи. В частности для рукописных и печатных цифро-буквенных символов оптимальным является тип полосовых признаков, обеспечивающий максимальную по сравнению с другими обобщающую способность.
Итак, первый этап обучения сводится к отысканию m оптимальных признаков j(L,X) первого уровня и фиксации m параметров L. Это позволяет на первом этапе распознавания преобразовать любое исходное изображение в некоторое промежуточное изображение с малым числом компонентов. Последующие процедуры выполняются с этими малокомпонентными изображениями.
Как следует из описания, в данном методе качество распознавания можно повышать путем ужесточения критериев на первом этапе, однако при этом значительно увеличивается время обучения. Важно понимать, что именно первый этап обучения существенно влияет на время обучения системы. Это происходит потому, что второй этап обучения (см. [1],[2],[3]) реализуется за счет перебора конечного числа точечных признаков, а именно 2m . Число всех этих признаков зависит, конечно, от числа признаков первого этапа m, и все-таки оно является конечным и относительно небольшим.
В противоположность признакам второго этапа обучения, которые выявляются из небольшого конечного числа точечных признаков, признаки первого этапа обучения (полосовые признаки) генерируются случайным образом, и процесс этот, при достаточно жестких критериях, может стать «бесконечным». Здесь следует уточнить, что на самом деле общее число полосовых признаков ограничено, но это число зависит от размера растра и для сколько-нибудь практических задач настолько велико, что при существующих вычислительных мощностях практически недостижимо. Например, для растра 32*32, общее число полосовых признаков составит 17976,93134861Е+304.
Экспериментально установлено, что при увеличении обучающей выборки частота оптимальных признаков быстро уменьшается. Таким образом, определенная модификация процедуры, осуществляющей генерацию полосовых признаков, проведенная так, чтобы частота оптимальных признаков первого этапа обучения увеличилась, является, по крайней мере, желательной.
Учитывая особенности решений, сгенерированных при помощи методов моделирования эволюции, имеет смысл использовать генетические алгоритмы (ГА) для поиска полосовых признаков, используемых на первом этапе обучения.
5. Генетическая модификация МООП
В работе [4] описаны модели наследственности и эволюции из области популяционной генетики. Эволюция осуществляется в результате взаимодействия трех основных факторов: изменчивости, наследственности и естественного отбора.
Генетический алгоритм (ГА) - это поисковый алгоритм, основанный на моделировании механизмов естественной эволюции. На каждом шаге генетического алгоритма создается новое множество решений, в котором используются части предыдущих решений и добавляются новые части. Таким образом генетические алгоритмы используют историческую информацию.
Основные отличия ГА состоят в следующем:
ГА осуществляют поиск из множества (популяции) точек, а не из единственной точки;
ГА используют целевую функцию для оценки информации, а не ее различные приращения.
Рассмотрим механизм простого ГА (ПГА): сначала ГА случайно генерирует популяцию последовательностей (стрингов); далее он копирует последовательности и переставляет их части; затем ГА применяет некоторые операторы к начальной популяции и генерирует новые популяции.
В ПГА используется 3 оператора: репродукция, кроссовер, мутация. Поясним кратко действие некоторых используемых генетических операторов.
Оператор Репродукции (ОР): механизм репродукции включает копирование стргингов. Репродукция - процесс, в котором стринги воспроизводятся согласно их функции фитности. Стринги с большим значением функции фитности имеют большую вероятность попадания в следующую генерацию. Один из способов алгоритмической реализации ОР – моделирование колеса рулетки, в котором каждый стринг имеет сектор, величина которого пропорциональна значению функции фитности стринга.
Оператор Кроссовера (ОК): оператор кроссовера может выполниться в 2 шага. На первом шаге элементы множества стрингов случайно разбиваются на пары. Затем из каждой пары стрингов формируется новая пара по правилу: случайно выбирается целочисленная позиция вдоль стринга между 1 и длиной стринга L - точка скрещивания. Новая пара стрингов создается вследствие обмена частями исходных стрингов, относительно точки скрещивания. Например, X и Y представляют собой два стринга (родители). Если теперь случайным или заранее заданным способом выбрать точку скрещивания, то смешивая части исходных векторов можно получить два новых потомка:X' и Y'.
X: x1 x2 x3 x4 x5 |x6 x7 x8
Y: y8 y7 y6 y5 y4 |y3 y2 y1
X': x1 x2 x3 x4 x5 |y3 y2 y1
Y': y8 y7 y6 y5 y4 |x6 x7 x8