Реферат: Основные понятия и определения теории графов

0, если вершина x_i не связана дугой с вершиной x_j

h_ij =

1, если вершина x_i связана дугой с вершиной x_j

Например, матрица [H] некоторого графа (рис.1, в) имеет следующий вид:

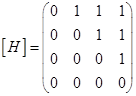
Структурной матрицей, называется матрица, которая соответствует некоторому графу G = (k, q), состоящему из n вершин k_i (i = 1, 2, …, n) и из m дуг q_j (j = 1, 2, …, m), называется матрица [S] порядка (nЧm) с элементами

-1, если дуга q_j выходит из вершины k_i

s_ij = +1, если дуга q_j входит из вершины k_i

0, если дуга q_j не инциндентна вершине k_i

В качестве примера составим структурную матрицу для того же графа приведенного на рис.1, в.

j1 2 3 4 5 6

b

i

d

c

[S] =

a

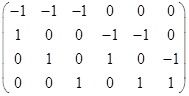
Потоковые графы

Каждой ХТС можно поставить в соответствие потоковый граф, гомоморфный рассматриваемой системе и являющийся некоторой топологической моделью одного типа обобщенных или физических потоков данной системы (рис.3). Потоковые графы строят для установившихся технологических режимов.

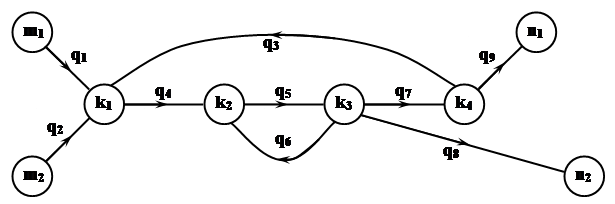
Рис.3. Потоковый граф ХТС.

Потоковый граф G = G (A) = (A, T) состоит из множеством вершин А, и образован совокупностью элементов, источников и стоков ХТС, и множеством дуг Т. Его элементы соответствуют одного типа обобщенным или физическим потокам системы. Потоковый граф представляет собой некоторое семейство сочетаний или пар вида Т = (а, b), где a Є A, b Є A, указывающее, какие вершины графа являются смежными. Можно выделить три типа потоковых графов ХТС: материальные, тепловые (энергетические), параметрические.

Вершины материального потокового графа по массовому расходу физических потоков (некоторого химического компонента) соответствуют элементам ХТС, которые трансформируют общие массовые расходы физических потоков (химического компонента), источникам и стокам веществ (компонента). Дуги данного графа отвечают обобщенным материальным потокам.

Вершины теплового потокового графа соответствуют элементам системы, которые изменяют расходы тепла физических потоков, внешним и внутренним источникам и стокам тепла ХТС.

Основные особенности материальных потоковых графов и тепловых потоковых графов. 1) ориентированность; 2) ассиметричность, т.к. не все соседние элементы системы связаны между собой обратными технологическими потоками; 3) связность, т.к. все элементы в системе взаимосвязаны единой цепью потоков веществ и энергии.

Параметрические потоковые графы являются топологической моделью, отображающей преобразование элементами системы параметров физических потоков ХТС. Вершины таких графов отвечают элементам, представляющим собой технологические операторы, которые качественно и (или) количественно преобразуют параметры физических потоков, а также источникам и стокам физических потоков ХТС. Дуги графа соответствуют физическим потокам системы. Такие графы являются конечными, ориентированными, ассиметричными, связными.

В работах Кафарова с сотрудниками предлагается строить потоковые графы, для которых известны технологическая топология и цель функционирования системы по следующему сценарию.

1. Изучить физико-химическую сущность технологических процессов ХТС и построитьее операторную схему.

2. Составить таблицу источников и стоков ХТС.

3. Составить матрицу [K] покомпонентного состава физических потоков системы. Общий элемент такой матрицы 1, если j-ый химический компонент входит в состав i-го физического потока к_ij = 0, в противном случае причем i = 1 – n – число физических потоков ХТС; j = 1 – m – число химических компонентов системы.

4. Составить таблицы одного типа материальных и тепловых обобщенных потоков системы.

5. Составить таблицы соответствия элементов, источников и стоков системы вершинам ее потокового графа.

6. Составить таблицы соответствия одного типа обобщенных потоков и физических ХТС дугам ее потоковых графов.

7. Графически изобразить потоковые графы ХТС.