Реферат: Перестановки

Для обозначим множество всех перестановок степени n таких, что . Число всех беспорядков степени n равно числу всех перестановок степени n не принадлежащих множеству . Обозначим число всех беспорядков степени n. По формуле включения- исключения

, (1)

где суммирование ведётся по всем кортежам Nтаким, что

. Легко видеть, что для любого кортежа N, где справедливо равенство

.

При фиксированном k число всех кортежей N, где , равно . Из равенства (1) следует, что

.

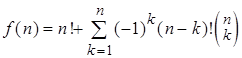Поэтому

.

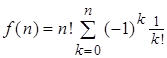п.3. Перестановки с повторениями.

Определение. Кортеж t = (b, ..., b) называется перестановкой с повторениями состава (n, ..., n) множества {a, ..., a}, если элемент a входит в t n раз, ..., a входит в t n раз, где n, ..., nÎN, .

Обозначение. Обозначим P(n, ..., n) число всех перестановок с повторениями состава (n, ..., n) некоторого k - элементного множества, где n = = n+...+n.

Теорема 1. Для любого (n, ..., n)ÎN

P(n, ..., n) = n!/n!...n! , где n = n+...+n .

Доказательство. Перестановка (b, ..., b) состава (n, ..., n) множества {a, ..., a} кодируется кортежем длины k: на первом месте кортежа записано множество тех мест в перестановке на которых расположен элемент ; на втором месте кортежа записано множество тех мест в перестановке, на которых расположен элемент ; ...; на k - ом месте кортежа записано множество тех мест в перестановке, на которых расположен элемент . Первый элемент кортежа может быть выбран способами; если первый элемент выбран, то второй можно выбрать 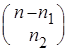способами; ...; если первые элементов выбраны, то k- ый элемент может быть выбран 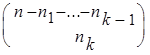способами. По правилу произведения получаем, что число всех перестановок с повторениями состава (n, ..., n) из {a, ..., a} равно

P(n, ..., n) = ...=

=

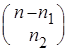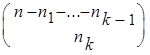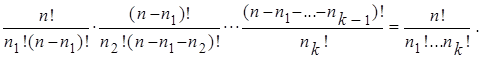
Обозначение. Для " n, ..., nÎN полиномиальный коэффициент 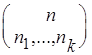определяется равенствами:

если n +...+ n = n, то ;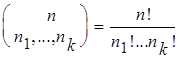

если n +...+ n¹ n, то .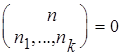

Следствие 1. Пусть A и B- конечные множества такие, что |A| = n, |B| = k, (n, ..., n)ÎN, n +...+ n = n, B = {b, ..., b}. Тогда число всех функций

f:A®B таких, что |f (b)| = n для всех i = 1, ..., k, равно .

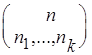Доказательство. Пусть A={a, ..., a}. Запишем функцию f:A®B в табличном виде .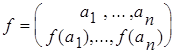

Кортеж (f(a), ..., f(a)) есть перестановка с повторениями состава (n, ..., n) множества {b, ..., b}.

Следствие 2. Пусть U- конечное множество, |U| = n. Тогда число кортежей множеств (A, ..., A) таких, что

|A| = n, ..., |A| = n,

|AÇA| = Æ для всех i ¹ j,

AÈ...ÈA = U, равно.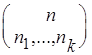

Доказательство. По теореме 2 п.3 число таких кортежей равно