Реферат: Принципы томографии
Заключение
Список литературы
Из истории МРТ
История МРТ начинается приблизительно в 1946 году, когда Феликс Блох открыл новые свойства атомного ядра, за что ему была присуждена Нобелевская премия. Он установил, что ядро ведет себя подобно магниту, а заряженная частица, такая как протон, вращающаяся вокруг собственной оси, имеет магнитное поле, известное как магнитный момент ядра. Открытие было сведено им в уравнение, названное уравнением Блоха. Теоретические исследования были подтверждены экспериментально в начале 1950-х годов. В 1960 году были разработаны спектрометры ядерно-магнитного резонанса для аналитических целей. На протяжении 1960 и 1970 годов ЯМР спектрометры широко использовались в академических и индустриальных исследованиях. Спектрометрия используется для анализа молекулярного строения вещества, основанного на его ЯМР спектре.
В конце 1960 годов Раймонд Дамадиан обнаружил, что злокачественная ткань отличается от нормальной ЯМР параметрами. Он предположил, что на основании этих различий можно характеризовать ткани. Опираясь на это открытие, в 1974 году он получил первое ЯМР изображение опухоли у крысы. В 1977 году Дамадиан и его помощники сконструировали первый сверхпроводящий ЯМР сканер и получили первое изображение тела человека, сканирование которого заняло почти 5 часов.
Одновременно Пол Лаутербур проводил подобные исследования в этой же области. Вопрос о том, кто же является родоначальником МРТ спорный, хотя, следует признать, что оба ученых внесли свой вклад.
Годом основания магнитно-резонансной томографии принято считать 1973, когда профессор химии Пол Лотербур опубликовал в журнале Nature статью «Создание изображения с помощью индуцированного локального взаимодействия; примеры на основе магнитного резонанса». Позже Питер Мэнсфилд усовершенствовал математические алгоритмы получения изображения.
Впоследствии в начале 1980 годов почти каждый производитель оборудования для получения медицинских изображений разрабатывал и производил МР сканеры. За изобретение метода МРТ в 2003 Питер Мэнсфилд и Пол Лотербур получили Нобелевскую премию в области медицины. Томография позволяет визуализировать с высоким качеством головной, спинной мозг и другие внутренние органы. Современные методики МРТ делают возможным неинвазивно (без вмешательства) исследовать функцию органов — измерять скорость кровотока, тока спинномозговой жидкости, определять уровень диффузии в тканях, видеть активацию коры головного мозга при функционировании органов, за которые отвечает данный участок коры (функциональная МРТ).
Почему МРТ?
Изображение тела пациента, полученное с помощью рентгеновского излучения, малоинформативно, так как обладает низким общим контрастным разрешением. Чтобы увеличить контраст изображения, можно менять контраст среды, применяя контрастные вещества на основе бария или йода. С помощью КТ сканеров можно получить изображения с гораздо большим контрастом для обнаружения поражений мягких тканей.
В большинстве случаев МРТ предоставляет гораздо более широкие возможности для диагностики, чем компьютерная томография. Так, магнитно-резонансная томография позволяет получить изображения высокой точности структуры головного и спинного мозга .
Также магнитно-резонансная томография лучше, чем компьютерная диагностика, выполняет анализ состояния мягких тканей – мышц, связок, жировой ткани, и так далее. Заболевания и нарушения внутренних органов, суставов и костей также прекрасно определяются при МРТ диагностике, но вот состояние полых органов (легких, кишечника, желудка и т.д.) лучше проверять при помощи компьютерной томографии. Принцип МРТ основан на резонировании атомов водорода, а полости, таким образом, аппарату практически неподвластны. Однако при использовании специальной рентгеновской пленки пространственное разрешение рентгеновских изображений отличное. Это особенно полезно при исследовании структуры кости.
В этом случае пространственное разрешение МРТ уступает рентгену.
Вообще, рентген и КТ используются для визуализации структуры кости, тогда как МРТ полезна для обнаружения повреждений мягких тканей.
Исследование МР томографии и устройство МР томографа
?????? ?????, ???????? ???????? ?????? ???????? ???????, ??? ??????? ???????? ??????? ?????????? (???????????) ????????? ????, ??????????????? ? ??????????? ????????? ????? ???? ????????. ??? ???????????? ????? ???? ???? ?????? ???????? ? ???? ????????, ??????? ???????????? ????? ????????? ?????????, ?????? ?? ????? ?????? ????????? ?????, ????????????? ???????????? ??????? ???????????? ???????? ???? ???????. ???????? ?????? ?????????? ????????? ???? ? ???????????? ?????????? ????, ???????? ???????, ??????????? ?. ???? ????????.????? ???????? ???????? ????????????, ?????? ??????? ????????? ???????????? ????? ???????, ????? ??????? ? ???? ???????? ????? ????????? ????? ??????? ????????? ? ???????? ?????????? ????? ????????? ????? ???????????? ??????????? ???????????? ?????????? ????. ????? ?? ????? ??????????? ????????? ???????? ???????????? ??????? ?????? ???????????? ? ???? ?????????????? ?????????, ??????? ?????????? ???????, ? ??? ????????????? ????? ???????? ????????? ?????????????? ???? ? ???????? ???????? ?????????.?????????????????? ???? ???????? ?? ?????????, ?. ????????????? ??????????? ? ???????????? ??? ?????????? (?????????????) ???.?????????????? ?????? ???????????? ????????? ???????????? ?????? ?? ????????? ????????:? ??????, ????????? ?????????? (???????????), ??? ?????????? ???????,? ????????? ????, ? ??????? ???????? ????????? ??????????? ???????, ????????? ?????? ?????????? ????????? ???? ? ??????????? ????? ????????? ???????, ?????????? ???????????, ??????? ????????? ??????? ??????? ???????????? ???? ???????? ?????????????? ??????? - ??????????, ???????????? ??? ???????? ??????????? ? ???? ????????, ? ???????? - ??? ??????????? ?????? ???????????? ????????? ?????????, ??????? ????????? ??????? ??????????? ? ?????????????? ???????, ???????????? ?????????? ???????, ???????????? ??, ?????????? ? ???? ?????? ? ?????????? ??? ????????????? ???.?????? ????????? ???? ??????????????? ????????? ?????????? ????, ??????? ?????????? В . ( [ B ] = 1 ?? )? ??? ? ??????????? ?? ???????? ??????????? ?????????? ???? ????????? ????????? ????? ??????????:? ?? ??????????? ????? 0,01 ?? - 0,1 ??? ?? ?????? ????? 0,1 - 0,5 ??? ? ??????? ????? 0,5 - 1.0 ??? ? ??????? ????? 1.0 - 2,0 ??? ?? ???????????? ????? >2,0 ??Физические основы явления ЯМР ??????? ? ?? ???????????? ???????, ??????? ????? ???????????? ??? ???????????? ??? ???????????. ????? ?????? ??????? ????????????? ??????? ????? ?????? ? ??????? ??????, ???????? ?? ????.
| Изотоп | Обозначение | Спиновое квантовое число | Гиромагнитное отношение (MГц/T) |
| Водород | 1 H | 1/2 | 42.6 |
| Углерод | 13 C | 1/2 | 10.7 |
| Кислород | 17 O | 5/2 | 5.8 |
| Фтор | 19 F | 1/2 | 40.0 |
| Натрий | 23 Na | 3/2 | 11.3 |
| Магний | 25 Mg | 5/2 | 2.6 |
| Фосфор | 31 P | 1/2 | 17.2 |
| Сера | 33 S | 3/2 | 3.3 |
| Железо | 57 Fe | 1/2 | 1.4 |
Энергетические уровни
Для понимания того, как частицы со спином ведут себя в магнитном поле, представим протон. Этот протон обладает свойством, называемым спином. Представим, что спин этого протона, является вектором магнитного момента, который заставляет протон вести себя как очень маленький магнит с северным и южным полюсами.
Когда протон помещен во внешнее магнитное поле, вектор спина располагается как магнит, по отношению ко внешнему полю. Состояние, когда полюса расположены N-S-N-S, является низкоэнергетическим , а N-N-S-S - высокоэнергетическим.
|
|
|
Переходы
Частица может подвергаться переходу между двумя энергетическими состояниями, поглощая фотон. Частица на нижнем энергетическом уровне поглощает фотон и оказывается на верхнем энергетическом уровне. Энергия данного фотона должна точно соответствовать разнице между этими двумя состояниями. Энергия протона, Е, связана с его частотой, 
, через постоянную Планка (h = 6.626x10-34 Дж с).
E = h
В ЯМР и МРТ величина называется резонансной или частотой Лармора.
Диаграммы энергетических уровней
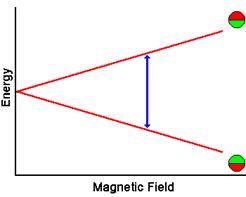Энергия двух состояний спина может быть представлена с помощью диаграммы энергетических уровней.
Известно, что = 
B и E = h , поэтому, для того, чтобы вызвать переход между двумя спиновыми состояниями, фотон должен обладать энергией
E = h B