Реферат: Прогнозирование критической температуры. Алканы и алкены
43
13
* n-количество соединений, участвовавших в определении значений i .
При этом следует иметь в виду, что прогнозирование Тс алканов с существенно большим по сравнению с рассмотренными структурами напряжением в молекуле может потребовать расширения таблицы кодовых чисел, что несложно сделать при наличии необходимых экспериментальных данных.
Корреляционная зависимость, характеризующая связь критической температуры с нормальной температурой кипения (Tb ) веществ и их индексами молекулярной связности (1-2 ), имеет вид
,(5.3)
где 
- суммарный индекс молекулярной связности второго порядка, вычисляемый по формуле
=
+
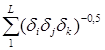,(5.4)
а - поправка на стерическое взаимодействие атомов углерода в разветвленных углеводородах, которые разделены тремя углерод-углеродными связями. Подобный подход использован Бенсоном (гл. 1) при введении “гош -поправок” в расчет энтальпий образования органических веществ. Расчет поправки производится в едином алгоритме Рандича для всех цепочек последовательно соединенных атомов, каждая из которых включает два и более третичных и (или) четвертичных атомов углерода, по формуле
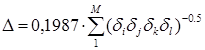,(5.5)
что эквивалентно 0,1987×
для взаимодействующих групп.
Некоторые примеры подобных цепочек углеродных атомов приведены на рис. 5.4.
Результаты прогнозирования 
алканов этим методом, приведенные в табл. 5.1, показывают, что среднее абсолютное отклонение расчетных значений от экспериментальных величин составляет 0,75 К, или 0,13% отн. И это при том, что только два параметра являются настраиваемыми по свойству, в связи с чем их оценки весьма представительны: в определении значений 
и 
участвовали 32 и 22 соединения соответственно. Максимальная погрешность расчета составляет 2,7 К, или 0,46% отн., из 66 соединений только 5 имеют погрешность, превышающую 2 К, и 17 - 1 К.
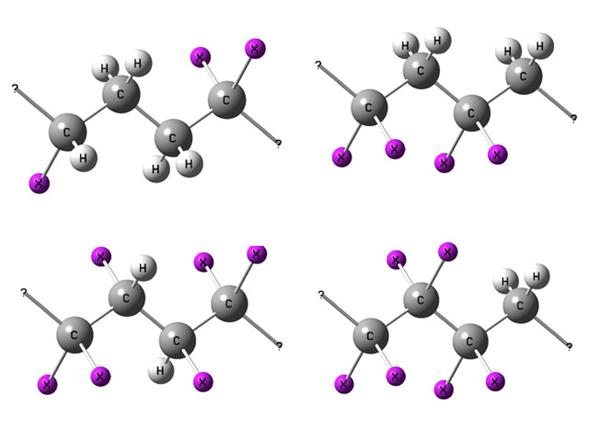
Р и с. 5.4. Примеры цепочек, включаемых в расчет поправок на стерическое взаимодействие
Анализ данных табл. 5.1 показывает, что из пяти рассмотренных методов лучшие результаты для представленной выборки веществ дает метод Марреро-Пардилло. Средняя абсолютная погрешность для него составляет 1,8 К, или 0,3% отн. Методы Лидерсена, Джобака, Константину-Гани и Вильсона-Джасперсона дают соответственно 3,1, 2,4, 6,2 и 7,8 К, или 0,5, 0,4, 1,1 и 1,4% отн. При этом обращает на себя внимание тот факт, что четыре метода из пяти (Лидерсена, Джобака, Константину-Гани и Марреро-Пардилло) дают значимо смещенные оценки Tc для некоторых групп линейных алканов. В случае метода Марреро-Пардилло положительное отклонение увеличивается от 5 до 16 К при переходе от нонадекана к докозану. Источником смещенных оценок в какой-либо области гомологических групп, как уже отмечалось, является избыточная “жесткость” принятого в методе вида корреляции. Опыт показывает, что использованная нами корреляция (ур-е 5.3) обладает большей гибкостью.
Результаты прогнозирования критической температуры алкенов, ароматических углеводородов, пиридинов, фенолов, спиртов изложены ниже.
Алкены
Класс алкенов представлен 29 соединениями, 16 из которых принадлежат линейным 1-алкенам, 4 - неразветвленным геометрическим изомерам и 9 имеют разветвление в молекуле. Таким образом, база данных по Тс алкенов весьма ограниченна. Это обстоятельство необходимо учитывать при прогнозировании критических температур алкенов с более сложным строением молекулы. Для совершенствования любого метода прогнозирования необходимо пополнение базы данных, в первую очередь, сведениями для соединений с разветвленными заместителями при двойной связи и - или - углеродных атомах.
Результаты прогнозирования Тс алкенов всеми рассматриваемыми методами приведены в табл. 5.5 и являются сопоставимыми, что говорит, скорее всего, не о близких прогностических возможностях методов, а об ограниченности сведений для их оценки.
Метод, основанный на индексах молекулярной связности Рандича, реализуется с использованием всего трех дополнительных кодовых чисел для выборки веществ, приведенной в табл. 5.5. Кодовые числа, являющиеся настроенными по свойству параметрами, представлены в табл. 5.4. Количество соединений, участвующих в процессе их определения, ³ 6, что характеризует удовлетворительный уровень достоверности получаемых при прогнозе результатов.
Расчет индексов молекулярной связности выполнялся по уравнению (5.3). Аналогично алканам при расчете индексов молекулярной связности разветвленных алкенов введены поправки, учитывающие взаимодействие углеродных атомов, разделенных четырьмя связями. Поправки вычислялись в едином алгоритме Рандича для всех цепочек последовательно соединенных атомов, каждая из которых включает два и более атомов углерода, имеющих разветвление. Для таких цепочек, включающих в свой состав хотя бы один углеродный атом с разветвлением, который, к тому же, находится при двойной связи, расчет поправки производился по формуле
,(5.6)
что эквивалентно 0,3334× для взаимодействующих групп.
Таким образом, уравнение (5.6) используется для геометрических изомеров, а также для 1-алкенов с заместителями в положениях 2 и 3 или 2 и 4. Для структур с разветвлением в молекуле при и т.д. атомах углерода расчет поправки производится по уравнению (5.5), как для разветвленных насыщенных структур.
Погрешность в оценках этим методом составляет 1,3 К, или 0,2 % отн. Максимальная погрешность – 4,6 К для 1-эйкозена. Обращает на себя внимание тот факт, что алкенилбензолы не требуют самостоятельных кодовых чисел для ненасыщенных -углеродных атомов.