Реферат: Распределение температуры по сечению балки
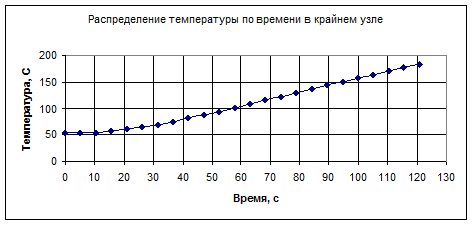
И так из результатов расчёта явным методом следует, что следует работать 73,47 сек, чтобы минимальная температура на противоположной стороне балки (узлы 6 и 10) была равна Tк =122˚С.
Расчет распределения температуры по сечению балки неявным методом
Основной недостаток явного численного метода состоит в том, что разностные уравнения баланса энергии для каждого узла должны удовлетворять критерию устойчивости. Чтобы удовлетворять критерию устойчивости в практике приходится выбирать очень маленький шаг по времени, и это приводит к значительному возрастанию объёма расчётов. Рассмотрим другой метод, который является устойчивым при любых значениях чисел Biи Fo. Суть его заключается в том, что уравнение баланса, полученное для явного метода, модифицирует, выражая через температуру в момент времени τ+Δτ. В этом методе разностные уравнения необходимо записывать для всех узлов, поэтому метод получил название неявного. Данный метод в математике называют методом использования левых производных, т.к. производная по времени опраксимируется разностью. Очевидно, что существенное преимущество неявного метода - это отсутствие критериев устойчивости, а недостаток - необходимость решения системы алгебраических уравнений (в отличие от неявного метода в явном можно решать разностные уравнения отдельно для каждого узла).
1. (1+2Fo· (2+Bi)) · (T1 ) τ+ Δτ -2·Fo· (1/2· (T6 ) τ+ Δτ + (T2 ) τ+ Δτ + Bi·T∞ + 1/2·Ts ) - (T1 ) τ =0
2. (1+4Fo) · (T2 ) τ+ Δτ - Fo· ( (T1 ) τ+ Δτ + (T3 ) τ+ Δτ + (T7 ) τ+ Δτ + Ts ) - (T2 ) τ =0
3. (1+4Fo) · (T3 ) τ+ Δτ - Fo· ( (T2 ) τ+ Δτ + (T4 ) τ+ Δτ + (T8 ) τ+ Δτ + Ts ) - (T3 ) τ =0
4. (1+4Fo) · (T4 ) τ+ Δτ - Fo· ( (T3 ) τ+ Δτ + (T5 ) τ+ Δτ + (T9 ) τ+ Δτ + Ts ) - (T4 ) τ =0
5. (1+2Fo· (2+Bi)) · (T5 ) τ+ Δτ -2·Fo· (1/2· (T10 ) τ+ Δτ + (T4 ) τ+ Δτ + Bi·T∞ + 1/2·Ts ) - (T5 ) τ =0
6. (1+4Fo· (1+Bi)) · (T6 ) τ+ Δτ - 4·Fo· (1/2· (T1 ) τ+ Δτ + 1/2· (T7 ) τ+ Δτ + Bi·T∞ ) - (T6 ) τ =0
7. (1+2Fo· (2+Bi)) · (T7 ) τ+ Δτ -2·Fo· (1/2· (T6 ) τ+ Δτ +1/2· (T8 ) τ+ Δτ +Bi·T∞ + (T2 ) τ+ Δτ ) - (T7 ) τ =0
8. (1+2Fo· (2+Bi)) · (T8 ) τ+ Δτ -2·Fo· (1/2· (T7 ) τ+ Δτ +1/2· (T9 ) τ+ Δτ +Bi·T∞ + (T3 ) τ+ Δτ ) - (T8 ) τ =0
9. (1+2Fo· (2+Bi)) · (T9 ) τ+ Δτ -2·Fo· (1/2· (T8 ) τ+ Δτ +1/2· (T10 ) τ+ Δτ +Bi·T∞ + (T4 ) τ+ Δτ ) - (T9 ) τ =0
10. (1+4Fo· (1+Bi)) · (T10 ) τ+ Δτ - 4·Fo· (1/2· (T5 ) τ+ Δτ + 1/2· (T9 ) τ+ Δτ + Bi·T∞ ) - (T10 ) τ =0
1.95-0.460.000.000.00-0.230.000.000.000.00 120,21
0.231.92-0.230.000.000.00-0.230.000.000.00 119,6
0.00-0.231.92-0.230.000.000.00-0.230.000.00 119,6
0.000.00-0.231.92-0.230.000.000.00-0.230.00 119,6
0.000.000.00-0.461.950.000.000.000.00-0.23 120,21
0.460.000.000.000.001.98-0.460.000.000.00 1,23
0.00-0.460.000.000.00-0.231.95-0.230.000.00 0,61
0.000.00-0.460.000.000.00-0.231.95-0.230.00 0,61
0.000.000.00-0.460.000.000.00-0.231.95-0.23 0,61
0.000.000.000.00-0.460.000.000.00-0.461.98 1,23
шаг по пространству - 0.05
шаг по времени - 30.00
начальная температура - 54.0
Распределение температуры по сечению балки
| Время | Температура, град С, в узле | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 | 54 |
| 30 | 129,13 | 130,78 | 130,98 | 130,78 | 129,13 | 75,75 | 76,88 | 77,04 | 76,88 | 75,75 |
| 60 | 184,96 | 188,34 | 188,84 | 188,34 | 184,96 | 107,37 | 109,88 | 110,28 | 109,88 | 107,37 |
| 90 | 228,22 | 233,21 | 234,06 | 233,21 | 228,22 | 141,71 | 145,64 | 146,44 | 145,64 | 141,71 |
| 120 | 262,88 | 269,29 | 270,5 | 269,29 | 262,88 | 175,23 | 180,64 | 181,83 | 180,64 | 175,23 |
| 150 | 291,32 | 298,98 | 300,53 | 298,98 | 291,32 | 206,32 | 213,14 | 214,73 | 213,14 | 206,32 |
| 180 | 315,07 | 323,81 | 325,68 | 323,81 | 315,07 | 234,35 | 242,48 | 244,46 | 242,48 | 234,35 |
| 210 | 335,14 | 344,82 | 346,98 | 344,82 | 335,14 | 259,23 | 268,53 | 270,87 | 268,53 | 259,23 |
| 240 | 352,23 | 362,73 | 365,15 | 362,73 | 352,23 | 281,08 | 291,43 | 294,11 | 291,43 | 281,08 |
| 270 | 366,87 | 378,08 | 380,72 | 378,08 | 366,87 | 300,17 | 311,44 | 314,42 | 311,44 | 300,17 |
| 300 | 379,45 | 391,27 | 394,11 | 391,27 | 379,45 | 316,78 | 328,86 | 332,1 | 328,86 | 316,78 |
| 330 | 390,28 | 402,63 | 405,64 | 402,63 | 390,28 | 331,2 | 343,98 | 347,45 | 343,98 | 331,2 |
| 360 | 399,62 | 412,43 | 415,59 | 412,43 | 399,62 | 343,69 | 357,1 | 360,77 | 357,1 | 343,69 |
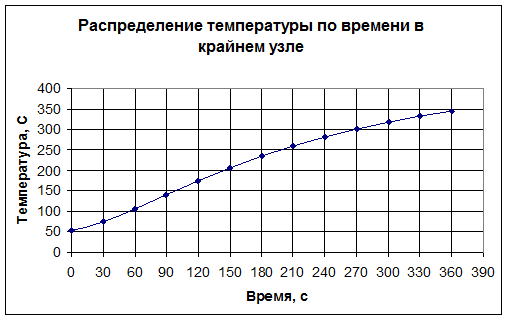
И так из результатов расчёта неявным методом следует, что следует работать 73,47 сек, чтобы минимальная температура на противоположной стороне балки (узлы 6 и 10) была равна Tк =122˚С.