Реферат: Равновесная кривая для товара повседневного спроса
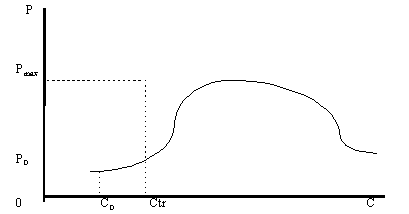
Рисунок 4. Проекция равновесной кривой на плоскость цена-доход. Первый случай.
Без доказательства приведу очевидное утверждение. Максимальная точка проекции равновесной кривой на плоскость объем-доход имеет в качестве координаты доход, при котором проекция равновесной кривой на плоскость цена-доход также соответствует максимуму.
2. Поверхность предложения СОВПАДАЕТ С линией максимального объема спроса
Чисто теоретически может существовать вариант, обозначенный на рисунке 2 цифрой 2. Что он означает? Этот случай возможен в том случае, когда линия максимальных объемов будет лежать не только на поверхности спроса, но и на поверхности предложения. То есть линия пересечения поверхностей спроса и предложения, которая является равновесной кривой, в некоторой своей части совпадет с линией максимальных объемов.
Этот случай следует признать мало вероятным. Действительно, ситуацию, когда максимально возможный объем спроса точно соответствовал технологическому максимуму возможностей фирм, следует признать практически невозможной. Тем не менее, если теоретически такая возможность существует, возможно, что и на практике придется с ней столкнуться. Поэтому следует этот случай разобрать, даже признавая его невероятным.
Равновесная кривая, полученная в этом случае, имеет очень необычный характер. Дело в том, что линия максимальных объемов для рассматриваемого товара уходит в бесконечность с увеличением в бесконечность цены товара и дохода потребителя. А так как равновесная кривая в своем максимальном положении совпадает с линией максимальных объемов, значит, что и равновесная кривая также уходит в бесконечность и имеет ограничение только по объемам.
Как и в предыдущем случае, рассмотрю не саму кривую в пространстве, а проекции кривой равновесия на плоскость объем-доход (рисунок 5) и плоскость цена-доход (рисунок 6).
Необычность поведения кривой равновесия обнаруживается уже на первой проекции, а именно на рисунке 5. Дело в том, что кривая равновесия представляет собой в данном случае уже сложную фигуру, а не кривую в строгом математическом смысле - одному значению фактора соответствует два значения аргумента и наоборот. До точки перелома, которая обозначена на рисунке 5, равновесная кривая ведет себя нормальным образом, однако при достижении поверхностью предложения линии максимальных объемов и совпадении с ней кривая раздваивается и превращается уже в фигуру, а не кривую.
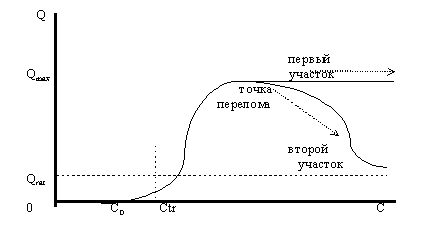
Рисунок 5. Проекция равновесной кривой на плоскость объем-доход. Второй случай.
Первый участок этой фигуры лежит на линии максимальных объемов и вместе с этой линией устремляется в бесконечность с увеличением дохода потребителя. На проекции фигуры на плоскость объем-доход этот участок показан прямой линией, параллельной оси доходов.
Второй участок фигуры также начинается в точке перелома и представляет собой равновесную линию, которая при росте дохода от точки перелома идет по поверхности спроса по линии убывания цен и объемов. Этот участок фигуры получается в результате пересечения поверхностью предложения той части поверхности спроса, которая лежит левее линии максимальных объемов. Эта часть соответствует нормальному расположению кривой равновесия в трехмерном пространстве.
Таким образом, полученная проекция равновесной кривой отличается от предыдущей проекции тем, что у нее появляется новый участок, который на рисунке 5 назван <первым участком>.
Примерно такая же сложная фигура будет получена, если равновесную кривую, получаемую посредством пересечения двух рассматриваемых поверхностей, спроецировать на плоскость цена-доход (рисунок 6).

Рисунок 6. Проекция равновесной кривой на плоскость цена-доход. Второй случай.
Она также начинается при доходе, равном С0, и при этом цена товара не равна нулю, а равна величине Р0, характеризующей себестоимость товара. Проекция фигуры, которую уже нельзя назвать кривой, имеет два участка.
Второй участок фигуры равновесия стремится с увеличением доходов к асимптоте, которая расположена параллельно оси доходов.
Первый же участок фигуры равновесия, изображенный на рисунке 6, совпадает с линией максимальных объемов, а значит, соответствует проекции этой линии на плоскость доход-цена.
И хотя ранее было сказано о том, что подобная ситуация маловероятна, полученные результаты все же требуют экономической интерпретации, так как полностью появление такой ситуации на практике исключить нельзя.
Осмысления требует, конечно, первый участок фигуры, совпавший с линией максимальных доходов, на котором равновесная кривая превратилась в прямую, уходящую в бесконечность. Для этого необходимо воспользоваться проекцией равновесной фигуры на третью плоскость - плоскость объем цена.
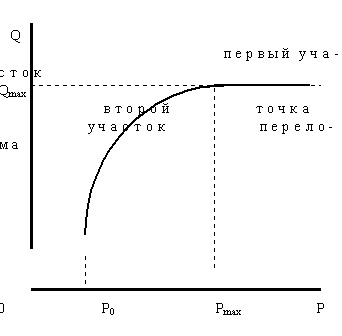
Рисунок 7. Проекция равновесной фигуры на плоскость объем-цена
Как было показано ранее, проекция фигуры совпадет с кривой предложения на этой плоскости (рисунок 7).
На рисунке наиболее интересна "точка перелома" - именно по достижении ее с дальнейшим ростом дохода равновесная кривая может совпасть с линией максимальных доходов (первый участок) или же, как и в предыдущем случае, с увеличением доходов будет иметь траекторию, характеризующуюся уменьшением цены и объемов.
Траектория равновесной кривой, совпадающая с линией максимальных объемов, характеризуется постоянным ростом цен, в то время как второй участок фигуры - снижением цен до определенного уровня рационального потребления.
Из этого следует, что первый участок характеризуется диктатом со стороны производителя товара, второй - диктатом со стороны потребителя. Иначе говоря, первый участок характерен для монополизма производителя, второй - для конкуренции и борьбы производителя за покупателя.
Так как полученная фигура характеризует рыночное равновесие, которое подвержено непрерывному изменению, то возможен ли одномоментный переход от первого участка ко второму? Этот переход будет характеризоваться резким падением объемов потребления и цен. На рисунке 6 это показано в правой его части стрелкой по штрих пунктирной линии.