Реферат: Решение систем нелинейных уравнений методом Ньютона
.
Следовательно, 
.
Внося эту правку в формулу (2.1), получим рабочую формулу метода Ньютона вида:
(2.2)
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой 
касательной, проведенной в некоторой точке 
этой кривой.
Для определенности положим 
и 
. Выберем начальное приближение 
, для которого . Проведем касательную к кривой в точке 
. За первое приближение 
берем точку пересечения касательной с осью 
. На кривой определим точку 
и проведем касательную к кривой в этой точке. Найдем следующее приближение 
и так далее (рис. 2.1).
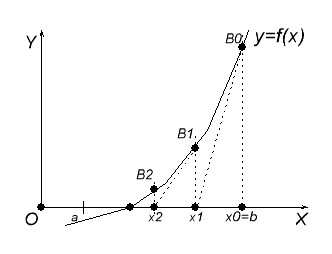
Рис. 2.1.
Составим уравнение касательной в точке 
:
.
Полагая 
, из уравнения касательной получим итерационную формулу метода Ньютона:
.
Если в качестве начального приближения взять другой конец отрезка 
, то следующее приближение 
.
Рассмотрим метод определения необходимого конца отрезка, выбираемого в качестве начального приближения 
.
Теорема. Если 
и производные 
не равны нулю и сохраняют определенные знаки на отрезке , то исходя из начального приближения , удовлетворяющего неравенству 
, по методу Ньютона, заданному формулой (2.2), можно вычислить единственный корень 
уравнения с любой степенью точности.
Доказательство.
Пусть для определенности 
при 
(остальные случаи рассматриваются аналогично).
Из неравенства 
следует, что 
, т.е. .
Докажем, что все приближения 
расположены правее , т.е. 
, а значит 
.
Доказательство проведем методом индукции:
а) 
;
б) предположим, что 
;
в) докажем, что 
.
Точное решение уравнения (1.1) можно представить в виде
.
Применяя формулу Тейлора, получим:
(2.3)
где 
.
Так как по условию теоремы , то последнее слагаемое в соотношении (2.3) положительное, следовательно,
.
Отсюда, в силу того, что 
, получим: